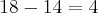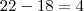por israel jonatas » Ter Nov 12, 2013 22:46
por israel jonatas » Ter Nov 12, 2013 22:46
O comandande de uma destacamento militar ordenou que seus subordinados se organizassem em filas. A primeira fila era composta por 14 soldados, a segunda por 18 soldados, a terceira por 22 soldados , e assim, sucessivamente. Sabe-se que o número de soldados deste destacamento é igual 1550. Dessa forma, é correto que serão formadas:
A) 18 filas
B) 20 filas
C) 23 filas
D) 25 filas
E) 30 filas
-
israel jonatas
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Mar 14, 2013 13:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Augusto Evaristo » Dom Nov 17, 2013 19:58
por Augusto Evaristo » Dom Nov 17, 2013 19:58
Matemática não é uma arte
É a linguagem universal
Arte é conhece-la!
-

Augusto Evaristo
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Out 15, 2010 18:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por israel jonatas » Seg Nov 18, 2013 22:44
por israel jonatas » Seg Nov 18, 2013 22:44
bom, R=4 usando a formula an= a1+(n-1)r ai fiquei por aqui pós tenho dúvidas no valor do N.
An= 1550 1550= 4+(n-1)4
A1= 4 1550=-4+4+4n
N=? 1550=4n
n=1550 N= 387,5
-
israel jonatas
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Mar 14, 2013 13:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Augusto Evaristo » Qua Nov 20, 2013 01:15
por Augusto Evaristo » Qua Nov 20, 2013 01:15
Muito bem. Você pensou na questão, e assim se aprende matemática. Pensando! Mas vamos pensar um pouco mais.
O n-esimo elemento (an) não pode ser 1550, pois este valor corresponde a quantidade de soldados. O primeiro elemento (a1) seria igual a 14, o número de soldados da primeira fila. Suas incógnitas são o numero de filas, n, e o n-esimo elemento, an.
an=a1+(n-1).r => an=14+(n-1).4
=> an=10-4.n
Sn=n. (a1+an)/2 => 1550=n. (14+an)/2
Substituindo an da 1a equação na 2a equação, temos:
1550=n. (14+10+4.n)/2, que dá em uma equação do segundo grau, n^2+6.n-775=0, cuja solução positiva é 25.
Logo, o total de filas a serem formadas são 25. Caso fosse pedido o e-nesimo elemento, era só substituir o valor de n em qualquer das duas primeiras equações.
Bons estudos!
Matemática não é uma arte
É a linguagem universal
Arte é conhece-la!
-

Augusto Evaristo
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Out 15, 2010 18:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por israel jonatas » Sex Nov 22, 2013 20:30
por israel jonatas » Sex Nov 22, 2013 20:30
Augusto Evaristo escreveu:Muito bem. Você pensou na questão, e assim se aprende matemática. Pensando! Mas vamos pensar um pouco mais.
O n-esimo elemento (an) não pode ser 1550, pois este valor corresponde a quantidade de soldados. O primeiro elemento (a1) seria igual a 14, o número de soldados da primeira fila. Suas incógnitas são o numero de filas, n, e o n-esimo elemento, an.
an=a1+(n-1).r => an=14+(n-1).4
=> an=10-4.n
Sn=n. (a1+an)/2 => 1550=n. (14+an)/2
Substituindo an da 1a equação na 2a equação, temos:
1550=n. (14+10+4.n)/2, que dá em uma equação do segundo grau, n^2+6.n-775=0, cuja solução positiva é 25.
Logo, o total de filas a serem formadas são 25. Caso fosse pedido o e-nesimo elemento, era só substituir o valor de n em qualquer das duas primeiras equações.
Bons estudos!
Perfeito fico muito grato. Muito obrigado mesmo, isso nos motiva ainda mais a busca por aprimoramento. Só uma dúvida é formula de PA é dividida por 2 certo, mas não seria 12 em vez de 6?
-
israel jonatas
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Mar 14, 2013 13:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Augusto Evaristo » Sáb Nov 23, 2013 18:54
por Augusto Evaristo » Sáb Nov 23, 2013 18:54
Olá!
A fórmula da soma dos n termos é:

Verifique que no desenvolvimento da expressão houve a simplificação de 24/2, que resulta em 12, mas há uma segunda simplificação 12/2 que o reduz para 6. Verifique ainda que ocorreram simplificações em todos os elementos da expressão.
Bons estudos!
Matemática não é uma arte
É a linguagem universal
Arte é conhece-la!
-

Augusto Evaristo
- Usuário Ativo

-
- Mensagens: 19
- Registrado em: Sex Out 15, 2010 18:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por israel jonatas » Sáb Nov 23, 2013 23:19
por israel jonatas » Sáb Nov 23, 2013 23:19
Augusto Evaristo escreveu:Olá!
A fórmula da soma dos n termos é:

Verifique que no desenvolvimento da expressão houve a simplificação de 24/2, que resulta em 12, mas há uma segunda simplificação 12/2 que o reduz para 6. Verifique ainda que ocorreram simplificações em todos os elementos da expressão.
Bons estudos!
Entendi, valeu mesmo.
-
israel jonatas
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qui Mar 14, 2013 13:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Lógica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- tenho dúvidas
por nayane » Sex Set 10, 2010 10:58
- 3 Respostas
- 2616 Exibições
- Última mensagem por Douglasm

Sáb Set 11, 2010 21:05
Geometria Plana
-
- também tenho dúvidas
por nayane » Sex Set 10, 2010 11:04
- 4 Respostas
- 2634 Exibições
- Última mensagem por nayane

Sáb Set 11, 2010 21:42
Trigonometria
-
- Resolver um problema que tenho duvidas
por amanda s » Dom Nov 17, 2013 16:39
- 2 Respostas
- 2017 Exibições
- Última mensagem por amanda s

Dom Nov 17, 2013 20:39
Cálculo: Limites, Derivadas e Integrais
-
- Tenho duvidas de como resolver este exercício!!!!
por Sarah_bernadeth » Sex Mar 28, 2008 18:47
- 1 Respostas
- 2218 Exibições
- Última mensagem por admin

Sex Mar 28, 2008 20:02
Álgebra Elementar
-
- Tenho dúvidas de como resolver este exercício de conjuntos
por Thiago Sousa » Ter Mai 06, 2008 17:11
- 2 Respostas
- 4576 Exibições
- Última mensagem por Thiago Sousa

Ter Mai 06, 2008 19:25
Conjuntos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.