mahhfe escreveu:Estou com dificuldades de resolver essa questão que "aparenta" não ser dificil
UECE 2001.2
Seja N = { 1, 2, 3, 4, ...) e f : A ---> N a função definidade por
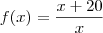
. Se

é o dominio mais amplo possível para f, a soma dos 5 menores elementos de A será:
a) 15
b) 18
c) 20
d) 22
Ps. é o meu primeiro post, estou tendo um pouco de dificuldades com os codigos, se algo estiver fora das regras ou codigos errados é só me falarem.
Primeiramente bem-vindo ao fórum! Faça bom uso...
Vamos lá quanto a questão:
Temos a seguinte função
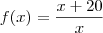
e queremos encontrar valores que quando substituirmos
x em
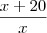
encontremos um número pertencente a N, ou seja, um número natural 1, 2, 3, ...
Não é difícil porque iremos fazer a seguinte "jogada"... Ao invés de usar
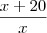
podemos escrever
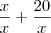
e por consequencia
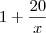
.
Ou seja,
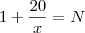
onde N é um número inteiro. Para isso dar inteiro a fração tem que ser redutível, sendo assim temos que encontrar os
x em que vamos dividir 20 e encontrar um número inteiro. Em outras palavras, quais são os 5 primeiros números que 20 é divisível?
Tente resolver agora.
A resposta certa é a letra d)
Qualquer dúvida informe aqui.
Bom estudo,

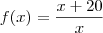 . Se
. Se  é o dominio mais amplo possível para f, a soma dos 5 menores elementos de A será:
é o dominio mais amplo possível para f, a soma dos 5 menores elementos de A será:

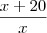 encontremos um número pertencente a N, ou seja, um número natural 1, 2, 3, ...
encontremos um número pertencente a N, ou seja, um número natural 1, 2, 3, ...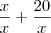 e por consequencia
e por consequencia 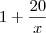 .
.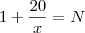 onde N é um número inteiro. Para isso dar inteiro a fração tem que ser redutível, sendo assim temos que encontrar os
onde N é um número inteiro. Para isso dar inteiro a fração tem que ser redutível, sendo assim temos que encontrar os 


 .
.
 :
: