 por Diego Silva » Sáb Jul 20, 2013 12:14
por Diego Silva » Sáb Jul 20, 2013 12:14
Me ajudem nessa questão?
Sejam u=(2,1,-3) e v=(1,-2,1)
a) Determine um vetor unitário simultaneamente perpendicular a u e v.
b) Determine um vetor w perpendicular a u e v tal que ||w||=5.
não sei como encontro perpendicular, no plano eu trocava as coordenadas e mudava o sinal de uma assim deixando perpendicular, no espaço não sei.
-
Diego Silva
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jun 11, 2013 18:22
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Química
- Andamento: cursando
 por e8group » Sáb Jul 20, 2013 12:51
por e8group » Sáb Jul 20, 2013 12:51
Dica : Designando
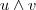
o produto vetorial entre os vetores
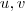
,temos que
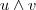
é simultaneamente ortogonal aos vetores mencionados acima . Assim , os vetores que estamos procurando dos itens (a) e (b) são paralelos a
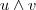
, ou seja , eles são múltiplos escalares de
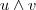
.Escreva então ,

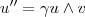
.
Onde :

Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Diego Silva » Sáb Jul 20, 2013 16:17
por Diego Silva » Sáb Jul 20, 2013 16:17
santhiago escreveu:Dica : Designando
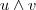
o produto vetorial entre os vetores
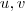
,temos que
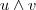
é simultaneamente ortogonal aos vetores mencionados acima . Assim , os vetores que estamos procurando dos itens (a) e (b) são paralelos a
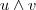
, ou seja , eles são múltiplos escalares de
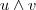
.Escreva então ,

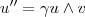
.
Onde :

Tente concluir .
não compreendi ao certo, se puder resolver entenderia melhor
-
Diego Silva
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jun 11, 2013 18:22
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Química
- Andamento: cursando
 por e8group » Sáb Jul 20, 2013 21:47
por e8group » Sáb Jul 20, 2013 21:47
O vetor
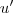
é unitário . Então ,

, ou seja ,

,logo
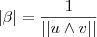
. Assim , os vetores
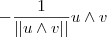
e

são simultaneamente ortogonais a
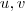
e unitários .Agora basta determinar o produto vetorial
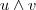
. Proceda da mesma forma para determinar o outro vetor de norma 5 .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Sáb Jul 20, 2013 21:55
por e8group » Sáb Jul 20, 2013 21:55
Alternativamente , você poderia supor que o vetor
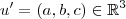
satisfaz as seguintes propriedades :
(a)
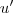
é unitário .
(b)
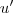
é simultaneamente ortogonal a
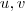
.
Os itens acima implicam ,
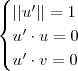
Agora é só fazer contas .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Diego Silva » Dom Jul 21, 2013 18:13
por Diego Silva » Dom Jul 21, 2013 18:13
acho que deixou claro, mas estou com muita dificuldade em Geometria Analítica, conseguindo resolver um consigo resolver semelhantes... se pudesse realmente resolver por completo.
-
Diego Silva
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jun 11, 2013 18:22
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Química
- Andamento: cursando
 por Diego Silva » Ter Jul 23, 2013 18:11
por Diego Silva » Ter Jul 23, 2013 18:11
consegui, obrigado!
-
Diego Silva
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Jun 11, 2013 18:22
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Química
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Vetor Unitario] questao de geometria analítica 1
por spektroos » Seg Set 24, 2012 01:41
- 2 Respostas
- 4378 Exibições
- Última mensagem por spektroos

Seg Set 24, 2012 16:52
Geometria Analítica
-
- Geometria analítica : Vetor unitário ortogonal
por isabellasimao » Sáb Abr 11, 2020 15:37
- 2 Respostas
- 5319 Exibições
- Última mensagem por isabellasimao

Qua Abr 15, 2020 15:14
Geometria Analítica
-
- [Vetor Unitario] Outra questao de geometria analítica 1
por spektroos » Seg Set 24, 2012 11:30
- 7 Respostas
- 5759 Exibições
- Última mensagem por spektroos

Seg Set 24, 2012 20:34
Geometria Analítica
-
- Geometria Analitica ( Vetor)
por raf » Qui Jun 11, 2015 03:46
- 1 Respostas
- 7715 Exibições
- Última mensagem por nakagumahissao

Sex Jun 12, 2015 15:37
Geometria Analítica
-
- vetor unitario
por andre barros » Sáb Mar 30, 2013 19:12
- 1 Respostas
- 1857 Exibições
- Última mensagem por e8group

Sáb Mar 30, 2013 20:50
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


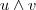 o produto vetorial entre os vetores
o produto vetorial entre os vetores 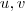 ,temos que
,temos que 
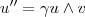 .
.

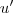 é unitário . Então ,
é unitário . Então ,  , ou seja ,
, ou seja , ,logo
,logo 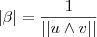 . Assim , os vetores
. Assim , os vetores 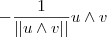 e
e  são simultaneamente ortogonais a
são simultaneamente ortogonais a 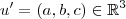 satisfaz as seguintes propriedades :
satisfaz as seguintes propriedades :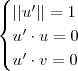
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
