 por amigao » Dom Mai 19, 2013 20:12
por amigao » Dom Mai 19, 2013 20:12
O triângulo ABC é retângulo em B e está contido em ?1: x+y+z=1. O cateto BC está contido em ?2:x-2y-2z=0 e a hipotenusa mede
![{2 \sqrt[ ]{6}}/3 {2 \sqrt[ ]{6}}/3](/latexrender/pictures/fa0c1c58b499d8e3b420df2773497a89.png)
. Sendo A=(0,1,0) determine B e C (o sistema de coordenadas é ortogonal).
O que eu fiz: Encontrei o diretor do cateto BC fazendo o produto vetorial das normais de cada plano, mas não consigo continuar.
-
amigao
- Usuário Dedicado

-
- Mensagens: 28
- Registrado em: Sáb Mai 11, 2013 11:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por young_jedi » Ter Mai 21, 2013 19:00
por young_jedi » Ter Mai 21, 2013 19:00
muito bem, fazendo o produto vetorial desse vetor diretor de BC com o vetor normal do plano
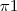
você encontra o vetor diretor de AB, vamos chamar esse vetor de v
com este vetor v você tem que que

onde B é um ponto pertencente a reta de intersecção dos dois planos, encontre essa reta e iguale nessa equação acima pra que você possa encontrar o valor de s e consequentemente o valor de B se tiver duvidas comente
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por RodrigoPorpino » Sex Out 24, 2014 20:29
por RodrigoPorpino » Sex Out 24, 2014 20:29
Brother young_jedi, pode detalhar mais detalhadamente? Não consigo resolver também. Obrigado
-
RodrigoPorpino
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Out 21, 2014 21:17
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- se um triangulo tem como vertices...
por willwgo » Seg Abr 18, 2011 17:44
- 2 Respostas
- 7916 Exibições
- Última mensagem por willwgo

Qua Abr 20, 2011 15:57
Geometria Analítica
-
- Geometria analitica - vertices do triangulo
por Dayannearaujo » Qui Abr 19, 2012 17:21
- 1 Respostas
- 2317 Exibições
- Última mensagem por LuizAquino

Sex Abr 20, 2012 00:07
Geometria Analítica
-
- Um triângulo têm como vértices os pontos A(5,3), B(4,2) e C(
por welton » Qui Out 23, 2014 14:40
- 1 Respostas
- 3442 Exibições
- Última mensagem por Russman

Qui Out 23, 2014 15:10
Trigonometria
-
- Duvida como achar a area do triangulo
 por renataf » Qui Dez 09, 2010 19:48
por renataf » Qui Dez 09, 2010 19:48
- 5 Respostas
- 4563 Exibições
- Última mensagem por Jefferson

Sáb Dez 11, 2010 22:45
Geometria Analítica
-
- [Cálculo] Problema triângulo
por pires_ » Dom Dez 09, 2012 16:22
- 2 Respostas
- 2559 Exibições
- Última mensagem por pires_

Dom Dez 09, 2012 20:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![{2 \sqrt[ ]{6}}/3 {2 \sqrt[ ]{6}}/3](/latexrender/pictures/fa0c1c58b499d8e3b420df2773497a89.png) . Sendo A=(0,1,0) determine B e C (o sistema de coordenadas é ortogonal).
. Sendo A=(0,1,0) determine B e C (o sistema de coordenadas é ortogonal).
![{2 \sqrt[ ]{6}}/3 {2 \sqrt[ ]{6}}/3](/latexrender/pictures/fa0c1c58b499d8e3b420df2773497a89.png) . Sendo A=(0,1,0) determine B e C (o sistema de coordenadas é ortogonal).
. Sendo A=(0,1,0) determine B e C (o sistema de coordenadas é ortogonal).
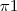 você encontra o vetor diretor de AB, vamos chamar esse vetor de v
você encontra o vetor diretor de AB, vamos chamar esse vetor de v

