a)
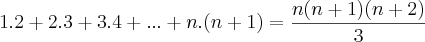
resp: para n=1
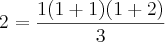 é verdade
é verdade estou mim atrapalhando para n=k+1
tem como mim ajudarem?
b)

resp: para n=1
 é verdade
é verdade mais para n=k+1, não sei fazer tem alguém que pode mim ajuda?

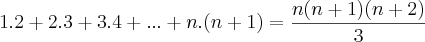
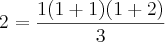 é verdade
é verdade 
 é verdade
é verdade 
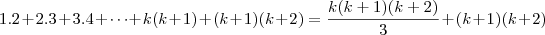










young_jedi escreveu:Até ai esta correto
voce tem que deixar na forma
sendo n=k+1
 se não for esta a resposta, por favor mim demostre onde estou errando.
se não for esta a resposta, por favor mim demostre onde estou errando.

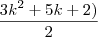
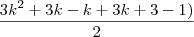
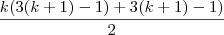
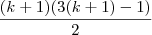

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.



