 por kawan » Qua Mar 27, 2013 17:49
por kawan » Qua Mar 27, 2013 17:49
Dados tres pontos A,B, e C nao - colineares , representar o vetor x -> nos casos
x= AB + 2BC
X=2CA+ 2BA
x= 3AB- BC
X= 1/2 AB - 2CB
Eu puiz em anexo como fiz a letra A to c duvida nessa parte me ajudem
- Anexos
-
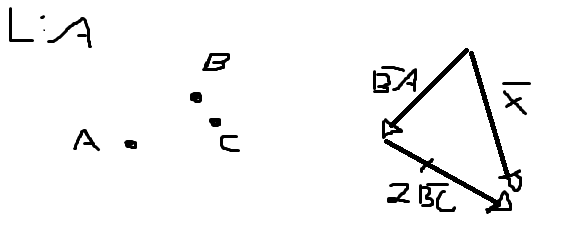
- Representaçao vetor.png (5.89 KiB) Exibido 5778 vezes
-
kawan
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Mar 27, 2013 17:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por timoteo » Qua Mar 27, 2013 17:54
por timoteo » Qua Mar 27, 2013 17:54
Editei imagem equivocada!
Editado pela última vez por
timoteo em Sex Mar 29, 2013 11:16, em um total de 1 vez.
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por kawan » Qui Mar 28, 2013 14:32
por kawan » Qui Mar 28, 2013 14:32
Nao entendi ! mas pede so pra representar tem como me mostrar como ficaria o exercicio completo? nao to entendeno
-
kawan
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Mar 27, 2013 17:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por timoteo » Qui Mar 28, 2013 19:31
por timoteo » Qui Mar 28, 2013 19:31
Editei imagem equivocada!
Editado pela última vez por
timoteo em Sex Mar 29, 2013 11:16, em um total de 1 vez.
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por kawan » Sex Mar 29, 2013 02:50
por kawan » Sex Mar 29, 2013 02:50
Mas o exercicio pede so pra mim representar vetor x em cada caso resolve pra mim como ficaria cada representaçao do x nas letras q passe lah tem como?
-
kawan
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Mar 27, 2013 17:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por kawan » Sex Mar 29, 2013 02:54
por kawan » Sex Mar 29, 2013 02:54
o anexo q puiz seria o resultado da letra A do exercico e os tres pontos q eu puiz sao como esta no exercicio para fazer ae manda representar x em cada caso lah...estou começo de g.a n sei mta coisa
-
kawan
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Mar 27, 2013 17:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por timoteo » Sex Mar 29, 2013 11:13
por timoteo » Sex Mar 29, 2013 11:13
O a forma que você representou o exercício é a maneira certa, pois está bem geral!
Mas, veja como você errou o sentido do vetor AB, a representação correta é assim:
Com esse primeiro resultado você pode chegar aos demais.
Tenha cuidado na hora da representação pois afeta o resultado!
No primeiro anexo eu estava equivocado!
Agora, espero ter ajudado!
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por Silva Lucas » Sex Mar 29, 2013 11:51
por Silva Lucas » Sex Mar 29, 2013 11:51
|x-1|<|x-2| (a regra e que eu posso elevar ao quadrado ambos os modulos. CERTO?
(|x-1|)ao quadrado <(|x-2|)ao quadrado
x*-2x+1 < x*-4x+4
lebrando q o * representa elevado ao quadrado... queria saber de onde veio o -2x e o -4x . qual a logica?
-
Silva Lucas
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Mar 28, 2013 15:21
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por timoteo » Sex Mar 29, 2013 12:04
por timoteo » Sex Mar 29, 2013 12:04
Seja bem vindo Lucas. Você tem que ler as regras do site. Não é permitido postar varias perguntas em um único post!
Então, da próxima escreva um post com sua dúvida. E utilize o editor de fórmulas para que você seja compreendido.
Pela sua pergunta vejo que você não sabe sobre potencia de polinômios, então, acho que você deveria olhar esse assunto!
Não se esqueça: até os grandes mestres revisam a base!
Respondendo a sua pergunta:

fazendo a multiplicação cruzada;

É isso ai!
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
 por Silva Lucas » Sex Mar 29, 2013 13:00
por Silva Lucas » Sex Mar 29, 2013 13:00
entendi, muito obrigado timoteo . Vou ler as regras e desculpa . Estou aprendendo ainda aqui com o site , mas aqui tem como add as pessoas? estava querendo umas aulas online , nao te interessa nao timoteo? remuneradas claro. tem algum email para contato?
-
Silva Lucas
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qui Mar 28, 2013 15:21
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por timoteo » Sex Mar 29, 2013 14:34
por timoteo » Sex Mar 29, 2013 14:34
Obrigado pelo convite, mas declino.
Talvez outros possam fazê-lo. Faça um post na parte de off-tópico!
É isso ai!
-
timoteo
- Colaborador Voluntário

-
- Mensagens: 117
- Registrado em: Ter Fev 14, 2012 07:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: bacharel matemática
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvidas com vetor unitário (versor)
por Ricardo HD » Sáb Abr 17, 2010 19:39
- 6 Respostas
- 7804 Exibições
- Última mensagem por MarceloFantini

Dom Jun 13, 2010 18:57
Geometria Analítica
-
- [CURVAS] ângulo entre vetor tangente e vetor posição
por inkz » Ter Nov 20, 2012 01:24
- 5 Respostas
- 4887 Exibições
- Última mensagem por LuannLuna

Qui Nov 29, 2012 15:05
Cálculo: Limites, Derivadas e Integrais
-
- [Curvas] Encontrar o vetor posição dado vetor aceleração
 por amigao » Sex Mai 09, 2014 16:37
por amigao » Sex Mai 09, 2014 16:37
- 1 Respostas
- 2078 Exibições
- Última mensagem por Russman

Sex Mai 09, 2014 17:25
Geometria Analítica
-
- [Vetor diretor] Encontrando um vetor diretor
por amigao » Sex Mai 17, 2013 13:19
- 2 Respostas
- 8376 Exibições
- Última mensagem por amigao

Sáb Mai 18, 2013 20:12
Geometria Analítica
-
- Vetor
por cristina » Ter Mai 11, 2010 09:54
- 2 Respostas
- 1967 Exibições
- Última mensagem por cristina

Ter Mai 11, 2010 18:22
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.










 fazendo a multiplicação cruzada;
fazendo a multiplicação cruzada; 




 .
.



