 tal que f'(x)=f(x). Encontrar (
tal que f'(x)=f(x). Encontrar ( (x)
(x) Não consegui chegar a um raciocínio muito coerente, tentei várias vezes e não está batendo com o gabarito (
 , x>0)
, x>0)Podem ajudar?

 tal que f'(x)=f(x). Encontrar (
tal que f'(x)=f(x). Encontrar ( (x)
(x)  , x>0)
, x>0)
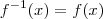 e ainda
e ainda  .
. ,existe uma função
,existe uma função  invertível,
invertível,  tal que
tal que  ,sendo assim ,
,sendo assim , 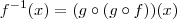 (Por quê ? ) . Mas ,
(Por quê ? ) . Mas , 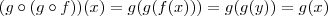 , daí
, daí 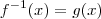 ,observe que
,observe que  pois
pois 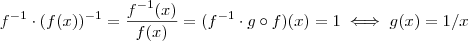 .
.
 (x) ser igual a f(x), e sim que a derivada de f(x) é igual a f(x).
(x) ser igual a f(x), e sim que a derivada de f(x) é igual a f(x).
 observe que
observe que 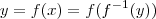 ,derivando ambos membros com respeito a
,derivando ambos membros com respeito a  ,
,  .
. 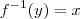

 que devido a hipótese
que devido a hipótese  resulta
resulta 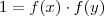 ,ou seja ,
,ou seja ,  ,logo ,
,logo , .
. e
e 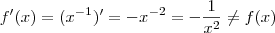 .
.


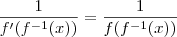
 ,
,  , x>0
, x>0
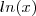 ? Pois,
? Pois, 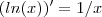 e pelo enunciado pede-se para encontrar
e pelo enunciado pede-se para encontrar  ,a menos que seja para encontrar
,a menos que seja para encontrar  (que neste caso a resposta é apenas
(que neste caso a resposta é apenas  ),mas para encontrar
),mas para encontrar 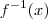 ,precisará integrar ambos membros com respeito a
,precisará integrar ambos membros com respeito a  ,caso você não conheça este conceito ,acredito que realmente o objetivo proposto pelo enunciado seja encontrar
,caso você não conheça este conceito ,acredito que realmente o objetivo proposto pelo enunciado seja encontrar  e não
e não  .
.
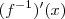 .Erro meu, desculpe!
.Erro meu, desculpe!
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes