Estou com um problema que envolve a estimação de posição e orientação de um objeto no espaço 3D, a partir de sua projeção 2D, no caso, um frame de vídeo, supondo conhecida a posição e orientação no frame anterior.
O problema é o seguinte:
Tenho alguns pontos 3D do objeto no instante (t-1):
![{P}_{i, t - 1} = {[ {X}_{i, t - 1} {Y}_{i, t - 1} {Z}_{i, t - 1} 1 ]}^{T} {P}_{i, t - 1} = {[ {X}_{i, t - 1} {Y}_{i, t - 1} {Z}_{i, t - 1} 1 ]}^{T}](/latexrender/pictures/81923f1d4825ecc50bda0a3e27463078.png)
Tenho os correspondentes pontos 2D no instante t:
![{p}_{i, t} = {[ {x}_{i, t } {y}_{i, t} ]}^{T} {p}_{i, t} = {[ {x}_{i, t } {y}_{i, t} ]}^{T}](/latexrender/pictures/dc3024dabc601f58927465b3c336cc39.png)
A transformação dos pontos do instante (t - 1) para o instante t é calculada por:
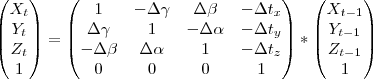
E a projecão 2D desses pontos é calculada por:
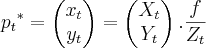
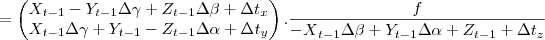
O objetivo é encontrar o valor de
![\Delta\mu = {[\Delta\alpha \Delta\beta \Delta\gamma \Delta{t}_{x} \Delta{t}_{y} \Delta{t}_{z} ]}^{T} \Delta\mu = {[\Delta\alpha \Delta\beta \Delta\gamma \Delta{t}_{x} \Delta{t}_{y} \Delta{t}_{z} ]}^{T}](/latexrender/pictures/65518e4b5873dddb0e41eb01e3f973e1.png) que minimize o erro:
que minimize o erro: 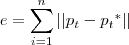
O problema é que ainda não consegui ver como aplicar mínimos quadrados a esse problema, que tem parâmetros tanto no numerados como no denominador.
É possível aplicar mínimos quadrados a um problema desse tipo? Como posso fazer isso? Ou, onde posso encontrar informações sobre como fazer isso?
Obrigado.

