 por marcosmuscul » Ter Mar 19, 2013 15:56
por marcosmuscul » Ter Mar 19, 2013 15:56
é uma questão sobre estudo do sinal de função.
no final ficou dois resultados como possíveis para o intervalo [1-?2,1+?2].
segue o a imagem da resolução digitalizada:

-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
 por marcosmuscul » Qui Mar 21, 2013 20:20
por marcosmuscul » Qui Mar 21, 2013 20:20
há algum nobre que possa me ajudar?
-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
 por e8group » Qui Mar 21, 2013 21:59
por e8group » Qui Mar 21, 2013 21:59
Desculpe mas não compreendi sua resolução ,não ficou claro .
Sua função é esta
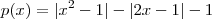
?
Se sim ,podemos retirar os módulos que por definição ,
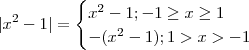
e

.
Façamos algumas observações :
Considere os intervalos
![I_1 = \left(-\infty ,-1 \right] , I_2 = \left(-1, -\frac{1}{2} \right) , I_3 = \left[ \frac{1}{2} , 1\right ) , I_4 = \left[ 1 ,+ \infty\right ) I_1 = \left(-\infty ,-1 \right] , I_2 = \left(-1, -\frac{1}{2} \right) , I_3 = \left[ \frac{1}{2} , 1\right ) , I_4 = \left[ 1 ,+ \infty\right )](/latexrender/pictures/21bc3333453853fea2041315171edbe8.png)
.
Temos :
i) Em

e
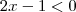
ii) Em

e
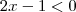
iii) Em

e
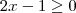
iv) Em

e
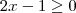
Assim ,obtemos

Faça o estudo do sinal da função em cada intervalo .Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por marcosmuscul » Sex Mar 22, 2013 00:14
por marcosmuscul » Sex Mar 22, 2013 00:14
Na verdade é
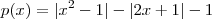
editei minha resolução pra tentar expor qual foi minha linha de raciocínio.

-
marcosmuscul
- Usuário Dedicado

-
- Mensagens: 39
- Registrado em: Ter Mar 19, 2013 15:48
- Localização: RJ
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: a começar engenharia civil
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Estudo de sinal dessa função]
por wilsonfilho0 » Ter Jun 14, 2016 17:06
- 1 Respostas
- 2283 Exibições
- Última mensagem por vitor_jo

Dom Jul 10, 2016 04:53
Funções
-
- Onde esta o meu erro
por VERTAO » Dom Mar 13, 2011 20:37
- 1 Respostas
- 2546 Exibições
- Última mensagem por Rogerio Murcila

Qua Mar 16, 2011 23:11
Matemática Financeira
-
- [Integral por partes] onde está o erro???
por Fabio Wanderley » Seg Mai 28, 2012 20:21
- 2 Respostas
- 2320 Exibições
- Última mensagem por Fabio Wanderley

Ter Mai 29, 2012 13:42
Cálculo: Limites, Derivadas e Integrais
-
- Expressões, onde esta o erro que eu não achei
por teilom » Sáb Ago 11, 2012 20:37
- 2 Respostas
- 3218 Exibições
- Última mensagem por teilom

Dom Ago 12, 2012 12:32
Equações
-
- Função ( Estudo do sinal )
por clara » Dom Jun 21, 2009 20:55
- 1 Respostas
- 5164 Exibições
- Última mensagem por Molina

Seg Jun 22, 2009 12:57
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





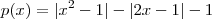 ?
? 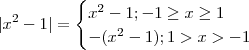
 .
.![I_1 = \left(-\infty ,-1 \right] , I_2 = \left(-1, -\frac{1}{2} \right) , I_3 = \left[ \frac{1}{2} , 1\right ) , I_4 = \left[ 1 ,+ \infty\right ) I_1 = \left(-\infty ,-1 \right] , I_2 = \left(-1, -\frac{1}{2} \right) , I_3 = \left[ \frac{1}{2} , 1\right ) , I_4 = \left[ 1 ,+ \infty\right )](/latexrender/pictures/21bc3333453853fea2041315171edbe8.png) .
.  e
e 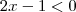
 e
e 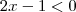
 e
e 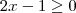
 e
e 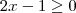


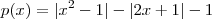




 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.