![\int_{a}^{b}\frac{dx}{x.\sqrt[]{{x}^{2}-b}} \int_{a}^{b}\frac{dx}{x.\sqrt[]{{x}^{2}-b}}](/latexrender/pictures/4c86720fab5fe7c4bae06986702ca588.png)
- Bom, segue a seguir como eu tentei resolver um problema prático que cai neste padrão - sem sucesso:
Cálculo 8ºed, HOWARD Anton, p.407:
![23) \int_{\sqrt[]{2}}^{2}\frac{dx}{x.\sqrt[]{{x}^{2}-1}} 23) \int_{\sqrt[]{2}}^{2}\frac{dx}{x.\sqrt[]{{x}^{2}-1}}](/latexrender/pictures/0be8461fc062c2ca85eacc43dcb43656.png)
- Realizando a substituição:
![u=\sqrt[]{{x}^{2}-1} u=\sqrt[]{{x}^{2}-1}](/latexrender/pictures/1ab9f42d8c65add3a3663dec558b40bd.png)

- Encontrando 'x' em termos de 'u':
![u=\sqrt[]{{x}^{2}-1} u=\sqrt[]{{x}^{2}-1}](/latexrender/pictures/1ab9f42d8c65add3a3663dec558b40bd.png)
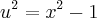

![x=\sqrt[]{{u}^{2}+1} x=\sqrt[]{{u}^{2}+1}](/latexrender/pictures/81b7439d721ee3e2de323da07b113525.png)
- Ajustando 'du':
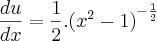


![\frac{du}{dx}=\frac{1}{2.\sqrt[]{{x}^{2}-1}} \frac{du}{dx}=\frac{1}{2.\sqrt[]{{x}^{2}-1}}](/latexrender/pictures/54615d0fc5629b34bc4dc83f6a83d55b.png)
![du=\frac{dx}{2.\sqrt[]{{x}^{2}-1}} du=\frac{dx}{2.\sqrt[]{{x}^{2}-1}}](/latexrender/pictures/48270038f2c2e6a6458a168b6cd60461.png)
![dx=du.2.\sqrt[]{{x}^{2}-1} dx=du.2.\sqrt[]{{x}^{2}-1}](/latexrender/pictures/17567e40dbbf70dadf3a0e277999edd6.png)
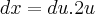
- Ajustando limite inferior:
![para: x=\sqrt[]{2} para: x=\sqrt[]{2}](/latexrender/pictures/f17748cc7d95967364041d9ddc9938f4.png)
![u=\sqrt[]{{(\sqrt[]{2})}^{2}-1} u=\sqrt[]{{(\sqrt[]{2})}^{2}-1}](/latexrender/pictures/1c5ca37575e8eb4e09869888b85af507.png)
![u=\sqrt[]{2-1} u=\sqrt[]{2-1}](/latexrender/pictures/eb207bb3ed7ac805db5380f20ebed268.png)
![u=\sqrt[]{1} u=\sqrt[]{1}](/latexrender/pictures/537a0a6493222b8a0ffb8af9a09422ef.png)

- Ajustando limite superior:

![u=\sqrt[]{{2}^{2}-1} u=\sqrt[]{{2}^{2}-1}](/latexrender/pictures/ffba68815d089bbdf1bfb868dcb5fac1.png)
![u=\sqrt[]{4-1} u=\sqrt[]{4-1}](/latexrender/pictures/33d72061d324698f4dbd51868436da15.png)
![u=\sqrt[]{3} u=\sqrt[]{3}](/latexrender/pictures/8e4042acd23b469ef88a7e251cb46f5d.png)
- Conclui-se então, que (considerando 'x' em termos de 'u'):
![\int_{\sqrt[]{2}}^{2}\frac{dx}{x.\sqrt[]{{x}^{2}-1}}=\int_{1}^{\sqrt[]{3}}\frac{du.2u}{\sqrt[]{{u}^{2}+1}.u} \int_{\sqrt[]{2}}^{2}\frac{dx}{x.\sqrt[]{{x}^{2}-1}}=\int_{1}^{\sqrt[]{3}}\frac{du.2u}{\sqrt[]{{u}^{2}+1}.u}](/latexrender/pictures/2fe50cc7433acad63c47520347deebf4.png)
![2.\int_{1}^{\sqrt[]{3}}\frac{du}{\sqrt[]{{u}^{2}+1}} 2.\int_{1}^{\sqrt[]{3}}\frac{du}{\sqrt[]{{u}^{2}+1}}](/latexrender/pictures/8be595226a1d999ca5c68c2ac77232fb.png)
- Sabendo que:
![\int_{}^{}\frac{dx}{\sqrt[]{{a}^{2}-{x}^{2}}}=arcsen\left(\frac{x}{a}\right) \int_{}^{}\frac{dx}{\sqrt[]{{a}^{2}-{x}^{2}}}=arcsen\left(\frac{x}{a}\right)](/latexrender/pictures/4fa31d225c1a1dc220e19fa755b941cb.png)
- Comparamos essa integral tabelada com a integral do problema, tendo que:

![\sqrt[]{{a}^{2}}=\sqrt[]{{u}^{2}} \sqrt[]{{a}^{2}}=\sqrt[]{{u}^{2}}](/latexrender/pictures/2590407c164f33148597f5e6e23a8552.png)


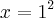

- Então:
![2.\int_{1}^{\sqrt[]{3}}\frac{du}{\sqrt[]{{u}^{2}+1}}=\left[2.arcsen\left(\frac{1}{u} \right) {{\right]}_{1}}^{\sqrt[]{3}} 2.\int_{1}^{\sqrt[]{3}}\frac{du}{\sqrt[]{{u}^{2}+1}}=\left[2.arcsen\left(\frac{1}{u} \right) {{\right]}_{1}}^{\sqrt[]{3}}](/latexrender/pictures/42fabd6040f00fa770782d2733fefdd6.png)
- Resolvendo a integral entre este intervalo:
![\left[2.arcsen\left(\frac{1}{\sqrt[]{3}} \right)\right]-\left[2.arcsen\left(\frac{1}{1} \right) \right] \left[2.arcsen\left(\frac{1}{\sqrt[]{3}} \right)\right]-\left[2.arcsen\left(\frac{1}{1} \right) \right]](/latexrender/pictures/1228e3d729357e1bbc0dbc1813317090.png)
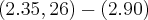

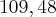
- Porém, a resposta do gabarito é:

- E agora, gente? Quem poderá me socorrer?
Grato, desde já.
Att. Matheus L. Oliveira




 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.