Resolva o sistema abaixo:
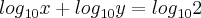
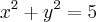
Obrigado.

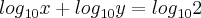
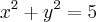

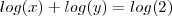

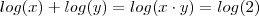 ou ainda que
ou ainda que  (OK ?)
(OK ?)![x^2 + y^2 = x^2 + y^2 + [2xy +(- 2xy)] = (x+y)^2 -2xy x^2 + y^2 = x^2 + y^2 + [2xy +(- 2xy)] = (x+y)^2 -2xy](/latexrender/pictures/78ce3ef875f77cab37c821ad06d844f6.png) .
.  substituindo-se em
substituindo-se em  obtemos que
obtemos que  .Extraindo a raiz quadrada em ambos membros
.Extraindo a raiz quadrada em ambos membros  . Visto que a equação (i) estar definida se , e somente se ,
. Visto que a equação (i) estar definida se , e somente se ,  são ambos positivos ,então ficamos apenas com
são ambos positivos ,então ficamos apenas com 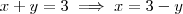 .
.  na equação (i) ou (ii) ,
na equação (i) ou (ii) ,
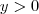 ,logo após substitua a solução p/
,logo após substitua a solução p/  em
em  e encontre
e encontre  .
.![[2xy +(- 2xy)] = 0 [2xy +(- 2xy)] = 0](/latexrender/pictures/5cf8923927d90c5effb2e75eaed9eb05.png) não estamos alterando o resultado (elemento neutro adtivo )
não estamos alterando o resultado (elemento neutro adtivo )![x^2 + y^2 = x^2 + y^2 + [2xy +(- 2xy)] x^2 + y^2 = x^2 + y^2 + [2xy +(- 2xy)]](/latexrender/pictures/7006b42c1a815a3688508daf5505bf2c.png) por associatividade temos que
por associatividade temos que ![x^2 + y^2 + [2xy +(- 2xy)] = (x^2 + y^2 +2xy) -2xy x^2 + y^2 + [2xy +(- 2xy)] = (x^2 + y^2 +2xy) -2xy](/latexrender/pictures/7788148cb259ef1b257cab237c933922.png) e ainda observando que
e ainda observando que  (OK?) , obtemos
(OK?) , obtemos  .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

