 por julia_cristina » Qui Nov 15, 2012 14:22
por julia_cristina » Qui Nov 15, 2012 14:22
Como resolver o exercício sen x = sen 3x.
Sabemos que a resposta é 45º mas não sabemos como chegar...
-
julia_cristina
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Nov 15, 2012 14:18
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: curso técnico em análise clinicas
- Andamento: cursando
 por DanielFerreira » Qui Nov 15, 2012 14:41
por DanielFerreira » Qui Nov 15, 2012 14:41
Sejam bem-vindas!
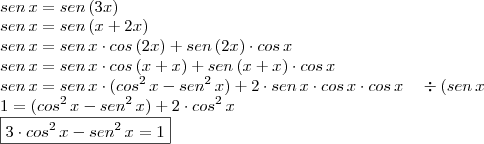
Sabemos que

, então:

Nota:

Espero ter ajudado!!
Comentem qualquer dúvida.
Daniel F.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por julia_cristina » Qui Nov 15, 2012 16:14
por julia_cristina » Qui Nov 15, 2012 16:14
Obrigada ajudou demais!!!!
-
julia_cristina
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Nov 15, 2012 14:18
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: curso técnico em análise clinicas
- Andamento: cursando
 por DanielFerreira » Qui Nov 15, 2012 20:29
por DanielFerreira » Qui Nov 15, 2012 20:29
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda Sistema Equação ENSINO FUNDAMENTAL
por olivergentris » Sáb Out 08, 2011 19:41
- 3 Respostas
- 2538 Exibições
- Última mensagem por joaofonseca

Dom Out 09, 2011 18:31
Sistemas de Equações
-
- Limite fundamental
por matmatco » Qui Set 01, 2011 11:04
- 6 Respostas
- 3465 Exibições
- Última mensagem por matmatco

Qui Set 08, 2011 10:19
Cálculo: Limites, Derivadas e Integrais
-
- [limite fundamental]
por TheKyabu » Qui Out 25, 2012 18:33
- 1 Respostas
- 1722 Exibições
- Última mensagem por TheKyabu

Qui Out 25, 2012 18:50
Cálculo: Limites, Derivadas e Integrais
-
- Ensino fundamental
por dolmian » Seg Dez 10, 2012 20:32
- 1 Respostas
- 1847 Exibições
- Última mensagem por young_jedi

Seg Dez 10, 2012 22:04
Álgebra Elementar
-
- Ensino fundamental
por dolmian » Seg Dez 10, 2012 20:35
- 1 Respostas
- 1371 Exibições
- Última mensagem por e8group

Seg Dez 10, 2012 21:49
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



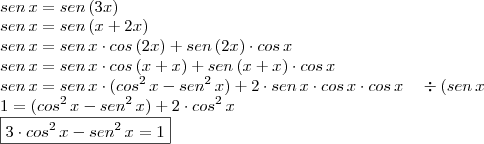
 , então:
, então:




