 por honorio » Dom Set 06, 2009 20:06
por honorio » Dom Set 06, 2009 20:06
Bem pessoal, estou com dificuldade em resolver esta questão, pois quando vou substituir a formula gerada por numero a resposta não dá certo.
a questão e a seguinte.
.Determine os valores dos numeros de barras com comprimento de 12m, ou seja, 1200cm, e o comprimento do complemento final conforme a figura abaixo.Sabento que
A, e o valor total e que 100cm corresponde ao transpasse, como mosta a figura abaixo, condições: complemento

1200cm e A>1200cm.

-
honorio
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Set 06, 2009 19:47
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: construção
- Andamento: formado
 por Marcampucio » Dom Set 06, 2009 23:45
por Marcampucio » Dom Set 06, 2009 23:45
Vejamos qual é o comprimento coberto à medida em que se colocam as barras:
1 barra - 1200
2 barras - 2300
3 barras - 3400
..
..
n barras - 1100(1+n)
Na verdade temos uma PA de razão
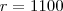
e

. Sendo

o comprimento total e

o complement0

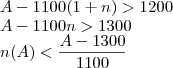
a expressão fornece

como o maior inteiro em função de

de tal modo que

por exemplo:
se queremos

a expressão fornece
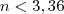
, portanto

e

,

Editado pela última vez por
Marcampucio em Seg Set 07, 2009 14:39, em um total de 2 vezes.
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por honorio » Seg Set 07, 2009 01:39
por honorio » Seg Set 07, 2009 01:39
Valeu caro Marcampucio, estava com este problema para resolver a mês, muito obrigado.
-
honorio
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Set 06, 2009 19:47
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: construção
- Andamento: formado
 por honorio » Seg Set 07, 2009 03:05
por honorio » Seg Set 07, 2009 03:05
Apos faser a verificação, da respostas, observei que apresenta falha, bem se A=5000, e dividi-lo por 1200 que representa o numero de peças com o mesmo tamanho, encontraremos 4, que tambem representa o numero de transpasse, entao o total de comprimento do complemento é =(4x100)+(5000-(1200x4) que sera 600. Este valores corresponde ao exemplo citado, esta faltando algum detalhe na resolução.
-
honorio
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Set 06, 2009 19:47
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: construção
- Andamento: formado
 por Marcampucio » Seg Set 07, 2009 14:37
por Marcampucio » Seg Set 07, 2009 14:37
Olá,
de fato havia uma passagem errada e já consertei.
A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por honorio » Seg Set 07, 2009 23:14
por honorio » Seg Set 07, 2009 23:14
Boa, já fiz o teste e deu tudo certo, muito obrigado.
-
honorio
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Set 06, 2009 19:47
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: construção
- Andamento: formado
 por honorio » Dom Set 13, 2009 01:08
por honorio » Dom Set 13, 2009 01:08
Caro Marcampio um dos meus colegas de estudos informou que a resposta ainda não esta coerente, pois ele deu A o valor de 2252 e T = 63, porem a resposta
não confere. favor como posso resouver isto?
-
honorio
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Set 06, 2009 19:47
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: construção
- Andamento: formado
 por Marcampucio » Dom Set 13, 2009 01:53
por Marcampucio » Dom Set 13, 2009 01:53
A questão que você propôs originalmente era esta:
a questão e a seguinte.
.Determine os valores dos numeros de barras com comprimento de 12m, ou seja, 1200cm, e o comprimento do complemento final conforme a figura abaixo.Sabento que A, e o valor total e que 100cm corresponde ao transpasse, como mosta a figura abaixo, condições: complemento\leq1200cm e A>1200cm.
Ou seja:
1- o comprimento das barras era fixo em 1200
2- o transpasse era fixo em 100
a expressão funciona para essas condições. Se você agora propõe um transpasse de 63 cm está mudando as condições iniciais para as quais a expressão é válida.
Para A=2252 e T=100 tudo funciona normalmente:
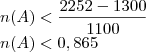
portanto

e

A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por honorio » Sáb Set 19, 2009 22:57
por honorio » Sáb Set 19, 2009 22:57
Tem a possibilidade de cria uma formula para qualquer valores para A, uma para o modulo principal no caso anterior 1200 que chamaremos de X, e o transpasse que sera Y.
-
honorio
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Set 06, 2009 19:47
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: construção
- Andamento: formado
 por Marcampucio » Dom Set 20, 2009 00:45
por Marcampucio » Dom Set 20, 2009 00:45
Tá. Passa uma borracha em tudo e fica com o que segue. Solução para qualquer caso.

A revelação não acontece ao encontrar o sábio no alto da montanha. A revelação vem com a subida da montanha.
-
Marcampucio
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Ter Mar 10, 2009 17:48
- Localização: São Paulo
- Formação Escolar: GRADUAÇÃO
- Área/Curso: geologia
- Andamento: formado
 por honorio » Dom Set 20, 2009 17:25
por honorio » Dom Set 20, 2009 17:25
Caro Marcampucio, utilizei o primeiro exemplo nesta formula e a resposta não foi a mesma, esta faltando alguma coisa, o mesmo acontecu com o exemplo do meu colega, estou vendo que para este caso não iremos obter sucesso, mais a luta continua, obrigado não irei descansar ate conseguir.
-
honorio
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Set 06, 2009 19:47
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: construção
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema matemático
por thiagocsouza » Ter Jan 03, 2012 22:41
- 8 Respostas
- 5031 Exibições
- Última mensagem por Arkanus Darondra

Sáb Jan 07, 2012 22:12
Sistemas de Equações
-
- Problema matematico
por girotto » Seg Jun 11, 2012 16:34
- 1 Respostas
- 1682 Exibições
- Última mensagem por Russman

Seg Jun 11, 2012 18:50
Sistemas de Equações
-
- problema matemático de vendas
por vb_evan » Sáb Mar 06, 2010 15:20
- 2 Respostas
- 3030 Exibições
- Última mensagem por vb_evan

Dom Mar 07, 2010 09:16
Dúvidas Pendentes (aguardando novos colaboradores)
-
- duvida em um problema matematico
por diogo_poa » Ter Mar 23, 2010 23:15
- 0 Respostas
- 1353 Exibições
- Última mensagem por diogo_poa

Ter Mar 23, 2010 23:15
Sistemas de Equações
-
- Porcentagem - Problema matemático
por Sheyla » Qua Mar 27, 2013 14:21
- 3 Respostas
- 3448 Exibições
- Última mensagem por Sheyla

Qua Mar 27, 2013 21:42
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 1200cm e A>1200cm.
1200cm e A>1200cm.


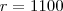 e
e  . Sendo
. Sendo  o comprimento total e
o comprimento total e  o complement0
o complement0
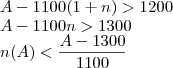
 como o maior inteiro em função de
como o maior inteiro em função de  a expressão fornece
a expressão fornece 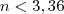 , portanto
, portanto  e
e  ,
, 

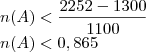
 e
e



 , avisa que eu resolvo.
, avisa que eu resolvo.

