A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por Molina » Sáb Jul 12, 2008 00:02
por Molina » Sáb Jul 12, 2008 00:02
Um Exército possuia um pelotão com apenas 10 combatentes, que neste caso serão representados por pontos. O Comandante deste pelotão ordenou que os combatentes se organizassem, formando 5 fileiras, cada uma contendo 4 combatentes. Como você organizaria o pelotão para que a ordem do Comandante seja cumprida?

Bom, trata-se de um problema matemático, ou seja, nota-se de imediato que para formar 5 fileiras contendo 4 combatentes cada uma, teríamos que ter 20 combatentes. Cabe a quem for tentar resolver pensar num modo "diferente" de posicioná-los.
Boa diversão!
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Molina » Sáb Jul 12, 2008 20:03
por Molina » Sáb Jul 12, 2008 20:03
Ninguém nem tentou fazer?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Roberta » Dom Jul 13, 2008 12:13
por Roberta » Dom Jul 13, 2008 12:13
oi Molina!
Só consegui pensar em formatos H, A, triangulos, cruz, ... apenas com 3 fileiras.

Vou aguardar a resposta

...
pensando mais um pouco .. cheguei a uma estrela, mas são 5 retas..

abs...
- Anexos
-
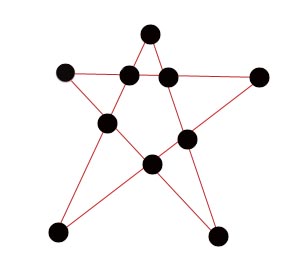
- 10ptos.jpg (35.72 KiB) Exibido 5659 vezes
Roberta.gmail

-
Roberta
- Usuário Parceiro

-
- Mensagens: 56
- Registrado em: Qui Jun 19, 2008 17:55
- Formação Escolar: GRADUAÇÃO
- Área/Curso: estudante de direito
- Andamento: cursando
 por Neperiano » Dom Jul 13, 2008 13:07
por Neperiano » Dom Jul 13, 2008 13:07
Boa Roberta ta certa
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Molina » Dom Jul 13, 2008 15:01
por Molina » Dom Jul 13, 2008 15:01
Isso mesmo roberta.
O problema traz 5 fileiras contendo 4 pontos cada.
Muito bem

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por admin » Dom Jul 13, 2008 17:00
por admin » Dom Jul 13, 2008 17:00
Olá!
Vocês podem pensar também que os pontos são intersecções entre duas retas.
E que cada reta teria que interceptar outras 4 em pontos distintos, ou seja, elas são concorrentes entre si em pontos distintos.
Sendo assim, o "formato" da figura não tem tanta importância, podemos começar traçando qualquer reta.
Em seguida, trace uma segunda reta concorrente à primeira.
Trace uma terceira que intercepta as outras duas, sempre em pontos distintos.
Trace uma quarta que intercepta as outras três.
E por fim, uma quinta que intercepta as outras 4.
Assim teremos 5 retas concorrentes entre si, em pontos distintos.
Qualquer formato de figura nestas condições será solução.
Um exemplo:
Abraços!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Desafios Fáceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Desafio dos Nove Pontos
 por Molina » Qua Jul 09, 2008 01:44
por Molina » Qua Jul 09, 2008 01:44
- 20 Respostas
- 47125 Exibições
- Última mensagem por Molina

Dom Mar 04, 2012 16:46
Desafios Fáceis
-
- [Pontos críticos - Derivadas] Ajuda com pontos críticos
por jonaskessinger » Qui Dez 13, 2012 18:16
- 1 Respostas
- 3585 Exibições
- Última mensagem por Russman

Qui Dez 13, 2012 19:35
Cálculo: Limites, Derivadas e Integrais
-
- Desafio
por Guarinense » Sex Nov 10, 2017 22:25
- 0 Respostas
- 5652 Exibições
- Última mensagem por Guarinense

Sex Nov 10, 2017 22:25
Teoria dos Números
-
- Desafio de lógica
por Twister » Qua Ago 13, 2008 21:46
- 10 Respostas
- 10034 Exibições
- Última mensagem por andymath

Qua Mar 31, 2010 19:14
Desafios Enviados
-
- Desafio do relógio
por ericomoura » Ter Nov 17, 2009 12:03
- 9 Respostas
- 8317 Exibições
- Última mensagem por Dan

Qui Fev 10, 2011 12:21
Desafios Difíceis
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.






 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
