por jose henrique » Sáb Out 09, 2010 15:40
por jose henrique » Sáb Out 09, 2010 15:40
O valor de
![\sqrt[]{x\sqrt[]{x\sqrt[]{x\sqrt[]{x.....}}}} \sqrt[]{x\sqrt[]{x\sqrt[]{x\sqrt[]{x.....}}}}](/latexrender/pictures/9f4d5ca8cc3c7be353e7b62278fab5f5.png)
é?
a questão diz que posso resolver com a equação limite da soma de um pg, mas eu não consegui nem armar.
a1= x
q=
![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
S=
![\frac{x}{1-\sqrt[]{x}} \frac{x}{1-\sqrt[]{x}}](/latexrender/pictures/0df0fb8dc255d4450c8e3a985daefbc5.png)
![\frac{x}{1-\sqrt[]{x}} . \frac{1+\sqrt[]{x}}{1+\sqrt[]{x}} =\frac{x+x\sqrt[]{x}}{1-x}
}{}}{} \frac{x}{1-\sqrt[]{x}} . \frac{1+\sqrt[]{x}}{1+\sqrt[]{x}} =\frac{x+x\sqrt[]{x}}{1-x}
}{}}{}](/latexrender/pictures/46dc560c00244f48e3c781f96ee4570f.png)
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por Douglasm » Sáb Out 09, 2010 17:38
por Douglasm » Sáb Out 09, 2010 17:38
Reescrevendo esse produto, notamos que ele é igual a:
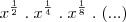
Ao multiplicarmos todos esses fatores, devemos somar os expoentes, que se encontram em progressão geométrica. A soma se dá por:

O produto é portanto igual a
x.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{x\sqrt[]{x\sqrt[]{x\sqrt[]{x.....}}}} \sqrt[]{x\sqrt[]{x\sqrt[]{x\sqrt[]{x.....}}}}](/latexrender/pictures/9f4d5ca8cc3c7be353e7b62278fab5f5.png) é?
é?![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
![\frac{x}{1-\sqrt[]{x}} \frac{x}{1-\sqrt[]{x}}](/latexrender/pictures/0df0fb8dc255d4450c8e3a985daefbc5.png)
![\frac{x}{1-\sqrt[]{x}} . \frac{1+\sqrt[]{x}}{1+\sqrt[]{x}} =\frac{x+x\sqrt[]{x}}{1-x}
}{}}{} \frac{x}{1-\sqrt[]{x}} . \frac{1+\sqrt[]{x}}{1+\sqrt[]{x}} =\frac{x+x\sqrt[]{x}}{1-x}
}{}}{}](/latexrender/pictures/46dc560c00244f48e3c781f96ee4570f.png)

![\sqrt[]{x\sqrt[]{x\sqrt[]{x\sqrt[]{x.....}}}} \sqrt[]{x\sqrt[]{x\sqrt[]{x\sqrt[]{x.....}}}}](/latexrender/pictures/9f4d5ca8cc3c7be353e7b62278fab5f5.png) é?
é?![\sqrt[]{x} \sqrt[]{x}](/latexrender/pictures/23c0d9674da78a0d1fae7f37c6ce8039.png)
![\frac{x}{1-\sqrt[]{x}} \frac{x}{1-\sqrt[]{x}}](/latexrender/pictures/0df0fb8dc255d4450c8e3a985daefbc5.png)
![\frac{x}{1-\sqrt[]{x}} . \frac{1+\sqrt[]{x}}{1+\sqrt[]{x}} =\frac{x+x\sqrt[]{x}}{1-x}
}{}}{} \frac{x}{1-\sqrt[]{x}} . \frac{1+\sqrt[]{x}}{1+\sqrt[]{x}} =\frac{x+x\sqrt[]{x}}{1-x}
}{}}{}](/latexrender/pictures/46dc560c00244f48e3c781f96ee4570f.png)