 por DanielRJ » Seg Out 04, 2010 15:28
por DanielRJ » Seg Out 04, 2010 15:28
Oá pessoal to com uma dificuldade nesta questão fiz varias e varias vezes e não obtive êxito.(UECE) Seja ( a1 , a2 , a3 ,.....) uma progressão geometrica crescente. Se
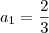
e
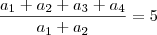
, então

é igual a:
a)14/3
b)28/3
c)10
d)20
Bom é isso pelos meus calculos aqui cheguei a esta expressãoo calculo da razão, então eria sabe onde cometi um equivoco: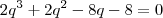
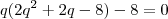
q=8 ,

,

,
 como é crescente
como é crescente 
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Seg Out 04, 2010 18:15
por MarceloFantini » Seg Out 04, 2010 18:15
Se é uma progressão geométrica crescente, então

. Essa informação será importante. Pelos dados do enunciado, temos que:

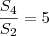
Vamos expandir a segunda equação:
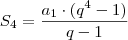

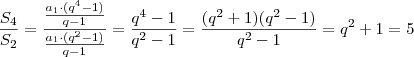
Logo,

.
Portanto,
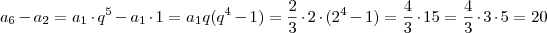
Alternativa D.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielRJ » Seg Out 04, 2010 22:44
por DanielRJ » Seg Out 04, 2010 22:44
Fantini escreveu:Se é uma progressão geométrica crescente, então

. Essa informação será importante. Pelos dados do enunciado, temos que:

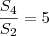
Vamos expandir a segunda equação:
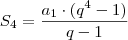

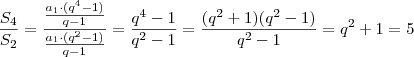
Logo,

.
Portanto,
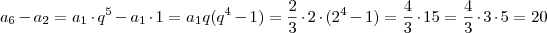
Alternativa D.
Bom obrigado. eu peguei as duas somas coloquei tudo em função de A1 e expandi. porque o resultado tambem não saiu correto?
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Seg Out 04, 2010 22:58
por MarceloFantini » Seg Out 04, 2010 22:58
Não entendi o que você quer dizer. Pode dar a dedução inteira?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielRJ » Seg Out 04, 2010 23:26
por DanielRJ » Seg Out 04, 2010 23:26
Fantini escreveu:Não entendi o que você quer dizer. Pode dar a dedução inteira?
Assim:

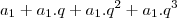
e depois substitui os
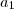
então queria saber porque não deu certo.
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por MarceloFantini » Ter Out 05, 2010 00:00
por MarceloFantini » Ter Out 05, 2010 00:00
teVeja se o que você tentou foi isso:
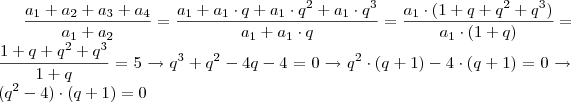
Daí, tiramos que
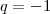
,
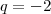
ou

. Como a progressão é crescente, a única possibilidade é

. Foi isso que você fez, ou que queria ter feito?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DanielRJ » Ter Out 05, 2010 01:18
por DanielRJ » Ter Out 05, 2010 01:18
Fantini escreveu:teVeja se o que você tentou foi isso:
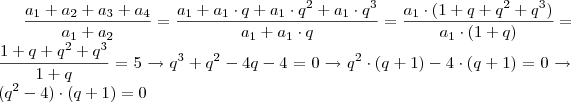
Daí, tiramos que
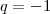
,

ou

. Como a progressão é crescente, a única possibilidade é

. Foi isso que você fez, ou que queria ter feito?
è foi isso mesmo percebi que coloquei em evidencia erradamente obrigado ¬¬
-

DanielRJ
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Sex Ago 20, 2010 18:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Progressao] série geometrica X progressao geometrica?
por aajunim » Seg Mar 18, 2013 11:19
- 2 Respostas
- 4254 Exibições
- Última mensagem por aajunim

Ter Mar 19, 2013 11:44
Progressões
-
- Progressão aritmética e progressão geométrica
por Danilo Dias Vilela » Sex Mar 12, 2010 13:41
- 1 Respostas
- 4726 Exibições
- Última mensagem por thadeu

Sex Mar 12, 2010 17:36
Progressões
-
- Progressão geométrica (ITA)
por Ananda » Sex Mar 07, 2008 13:27
- 17 Respostas
- 25556 Exibições
- Última mensagem por Ananda

Qui Mar 13, 2008 11:10
Progressões
-
- Progressão Geométrica
por nicecaps » Seg Mar 22, 2010 11:37
- 2 Respostas
- 4239 Exibições
- Última mensagem por nicecaps

Ter Mar 23, 2010 09:45
Progressões
-
- Progressão Geométrica
por Jessie » Qui Abr 29, 2010 17:49
- 1 Respostas
- 2892 Exibições
- Última mensagem por Elcioschin

Qui Abr 29, 2010 20:12
Pedidos
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
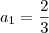 e
e 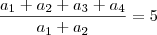 , então
, então  é igual a:
é igual a: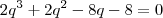
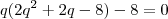
 ,
,  ,
, 



 . Essa informação será importante. Pelos dados do enunciado, temos que:
. Essa informação será importante. Pelos dados do enunciado, temos que:
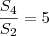
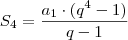

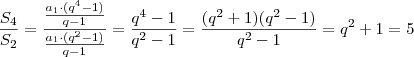
 .
.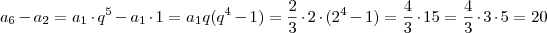



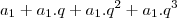
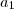 então queria saber porque não deu certo.
então queria saber porque não deu certo.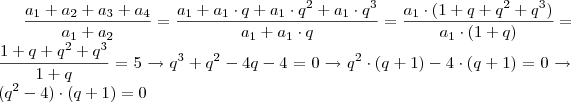
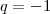 ,
,  ou
ou  . Como a progressão é crescente, a única possibilidade é
. Como a progressão é crescente, a única possibilidade é 

 , avisa que eu resolvo.
, avisa que eu resolvo.

