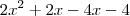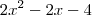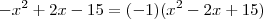por DanielFerreira » Qua Set 29, 2010 14:38
por DanielFerreira » Qua Set 29, 2010 14:38
Olá
José,
seu raciocínio foi certinho, você errou apenas a passagem de
Produtos Notáveis

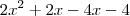
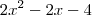
2x² - 2x - 4 = x² + 11
x² - 2x - 15 = 0
(x - 5)(x + 3) = 0
x - 5 = 0
x = 5
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por MarceloFantini » Qua Set 29, 2010 19:51
por MarceloFantini » Qua Set 29, 2010 19:51
Danjr, não notei o erro:
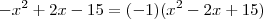
Como ambos são iguais a zero, é apenas uma questão de contas mais fáceis, tanto que as respostas foram as mesmas.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Elcioschin » Qua Set 29, 2010 20:29
por Elcioschin » Qua Set 29, 2010 20:29
Fantini
O danielcdd e o danjr acertaram.
Quem errou foi o José ao calcular o produto (x - 2)*(2x + 2) = 2x² - 2x - 4
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por MarceloFantini » Qua Set 29, 2010 20:37
por MarceloFantini » Qua Set 29, 2010 20:37
Ah. Obrigado pelo esclarecimento, Elcio.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jose henrique » Qui Set 30, 2010 08:08
por jose henrique » Qui Set 30, 2010 08:08
obrigado a todos !!
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por jose henrique » Qui Set 30, 2010 08:12
por jose henrique » Qui Set 30, 2010 08:12
obrigado a todos !!
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por MarceloFantini » Qui Set 30, 2010 21:26
por MarceloFantini » Qui Set 30, 2010 21:26
Jose Henrique, apenas note que a pergunta ainda não foi respondida, pois o problema pede pelo sétimo termo, não pelo x.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por jose henrique » Qui Set 30, 2010 21:38
por jose henrique » Qui Set 30, 2010 21:38
fantini, obrigado pelo o alerta. eu estava ciente disso mas a dúvida foi esclarecida. Peço novamente obrigado!
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
Voltar para Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![(x-2, \sqrt[]{{x}^{2}+11}, 2x+2, ...) (x-2, \sqrt[]{{x}^{2}+11}, 2x+2, ...)](/latexrender/pictures/f04b655c3876a0f2feca84acc71f32de.png) cujo o sétimo termo vale:
cujo o sétimo termo vale:![{\left(\sqrt[]{{x}^{2}+11} \right)}^{2}=\left(x-2 \right)\left(2x+2 \right) {\left(\sqrt[]{{x}^{2}+11} \right)}^{2}=\left(x-2 \right)\left(2x+2 \right)](/latexrender/pictures/509724bfb5679c5377a97ca117c8e1e1.png)

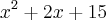
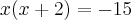
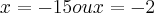

![(x-2, \sqrt[]{{x}^{2}+11}, 2x+2, ...) (x-2, \sqrt[]{{x}^{2}+11}, 2x+2, ...)](/latexrender/pictures/f04b655c3876a0f2feca84acc71f32de.png) cujo o sétimo termo vale:
cujo o sétimo termo vale:![{\left(\sqrt[]{{x}^{2}+11} \right)}^{2}=\left(x-2 \right)\left(2x+2 \right) {\left(\sqrt[]{{x}^{2}+11} \right)}^{2}=\left(x-2 \right)\left(2x+2 \right)](/latexrender/pictures/509724bfb5679c5377a97ca117c8e1e1.png)

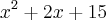
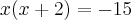
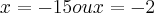


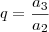
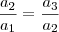
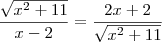



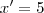 e
e 
 vamos espera a correção de um professor.
vamos espera a correção de um professor.