Olá, boas-vindas!
Desculpe a demora em responder. Além de meu foco ser as dúvidas do Ensino Médio, nestes últimos dias tivemos um problema com um dos componentes do LaTeX no site, impossibilitando a exibição de novas fórmulas. E percebi justamente ao tentar enviar esta resposta ontem.
Como "estudante", adotaria a seguinte postura para entender como proceder na resolução, fica como sugestão:
-Em primeiro lugar, estude o que é um subespaço vetorial.
Há um tópico aqui com uma discussão relacionada, pode ajudar:
viewtopic.php?f=117&t=296#p757-Também estude o que é uma base vetorial.
Você verá que os vetores da base são linearmente independentes.
E que todos os vetores do subespaço considerado são gerados por estes vetores da base.
Por exemplo, como a base de
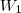
é

, a dimensão de
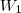
é

, e para cada vetor de
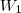
existe uma "m-upla" de escalares

tais que
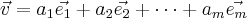
.
Quando eu escrevo para você "estudar o que é..." quero dizer para rever com atenção as definições e teoremas.
Em resumo, será necessário utilizar a existência destes escalares, juntamente com as condições de subespaço.
 contém apenas o vetor nulo. Seja {e1, ..., em} uma base de W1, e {e'1, ..., e'n} uma base de W2. Mostre que {e1, ..., em, e'1, ..., e'n} é uma base do subespaço W = W1 + W2, onde W1 + W2 é conjunto de todos os vetores de V da forma x1 + x2, onde x1 pertence a W1 e x2 pertence a W2. Mostre ainda que dim(W) = dim(W1) + dim(W2)
contém apenas o vetor nulo. Seja {e1, ..., em} uma base de W1, e {e'1, ..., e'n} uma base de W2. Mostre que {e1, ..., em, e'1, ..., e'n} é uma base do subespaço W = W1 + W2, onde W1 + W2 é conjunto de todos os vetores de V da forma x1 + x2, onde x1 pertence a W1 e x2 pertence a W2. Mostre ainda que dim(W) = dim(W1) + dim(W2)

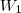 é
é  , a dimensão de
, a dimensão de  , e para cada vetor de
, e para cada vetor de  tais que
tais que 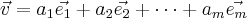 .
.
 W1, pode então ser escrito como :
W1, pode então ser escrito como :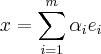 --------(1)
--------(1) ----------(2)
----------(2) =
= 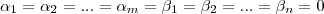
 } é L.I.
} é L.I. , logo:
, logo: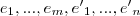 }
}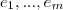 } é base de W1 --> Dim(W1) = m
} é base de W1 --> Dim(W1) = m } é base de W2 --> Dim(W2) = n
} é base de W2 --> Dim(W2) = n e
e 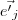 , faltou a notação de vetor.
, faltou a notação de vetor. fica dito que
fica dito que 

 , avisa que eu resolvo.
, avisa que eu resolvo.

