Olá Fernanda, seja bem-vinda!
Olá Maligno e Molina!
Permitam meus comentários na discussão.
Como o Maligno escreveu, bastaria calcular os volumes, um a um, e somar.
Mas, com razão, a Fernanda não quer ter este trabalho todo, fazendo as contas somando base X altura.
O Molina bem sugere que deve haver algo a mais na seqüência!
Pois bem, em primeiro lugar devo dizer que esta preocupação, em geral excessiva, com "fórmulas" é prejudicial no entendimento dos problemas.
Em muitos casos aplicamos sim fórmulas, mas antes precisamos entender a resolução. Muitas vezes, em vários exercícios, percebo que os alunos "sabem" alguma fórmula relacionada ao assunto, mas não sabem resolver o problema!
Neste exemplo, é evidente que há uma progressão aritmética e uma geométrica relacionadas. Mas também é fácil perceber que não basta saber as "fórmulas" da soma de termos de cada uma. Utilizaremos as tais fórmulas para facilitar? Talvez, vamos ver! Mas, somente após entendermos como esta seqüência se comporta. Vamos discutir esta idéia!
Embora estejamos procurando a soma dos volumes, no momento não são importantes os "resultados" dos volumes, mas sim, as operações que estão sendo feitas.
Para visualizarmos, vamos considerar alguns termos - os volumes:

Como eu disse, não nos interessa aqui que

é igual a
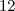
.
Vamos ao próximo termo!
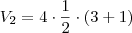
Mais um:
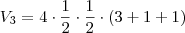
Outro:

E outro:

Acho que já podemos "generalizar" o volume, ou seja, encontrar o termo geral, vejam:
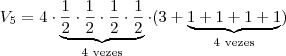
Ou seja:
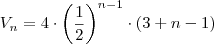
Simplificando ainda mais o termo geral, temos:
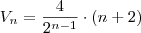
Este resultado deve ser provado por indução, mas acredito que não seja o foco deste exercício.
Mais simplificações:
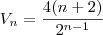


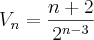
Assim, o termo geral para o volume está bem simplificado.
Como estamos interessados na soma, chamemos de
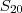
e vamos representá-la através do símbolo somatório:


Reparem que olhando para os numeradores e denominadores, isoladamente, temos uma PA e uma PG, respectivamente.
Mas, por ser uma soma de frações com denominadores diferentes, não podemos somar diretamente os numeradores, ou os denominadores, então, não podemos utilizar as tais fórmulas de soma de termos, exceto se algo ainda esteja ausente nesta minha tentativa.
Pelo menos assim fica mais "prático" obter a soma dos 20 volumes:


Reparem que os volumes ficam cada vez menores, pois há um aumento exponencial dos denominadores.
Pensando assim, já poderíamos obter um volume bem aproximado, sem somarmos todos os 20 termos da seqüência, apenas somando alguns iniciais.
Mas, vejamos agora os valores obtidos de forma prática com o termo geral:

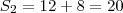

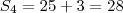
Como temos potências de 2, nesta resolução seria conveniente utilizar uma calculadora científica, pois os denominadores ficam maiores.






Vejam que este volume que estamos somando é bem pequeno e a soma já pouco aumenta.
Ao fazer na calculadora, é mais prático utilizar em cada soma o valor anterior retornado:

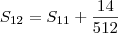


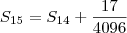
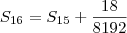
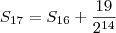
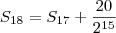
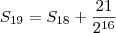
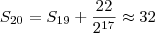
Dizemos que a soma dos volumes "converge" para
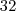
.
Bons estudos para todos!





 é igual a
é igual a 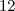 .
.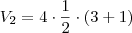
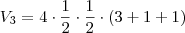


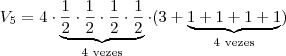
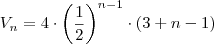
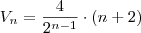
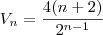


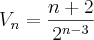
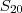 e vamos representá-la através do símbolo somatório:
e vamos representá-la através do símbolo somatório:




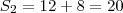

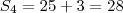







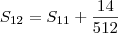


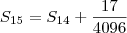
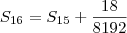
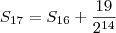
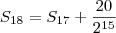
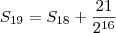
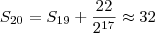
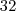 .
.