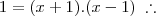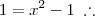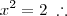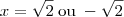por jose henrique » Seg Set 13, 2010 09:26
por jose henrique » Seg Set 13, 2010 09:26
Se x é positivo e se o inverso de x+1 é x-1 determine o valor de x
como faço para encontrar o valor dessa equação?
Seria isso

e depois disso como faço?
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por Elcioschin » Seg Set 13, 2010 11:07
por Elcioschin » Seg Set 13, 2010 11:07
O que você escreveu NÃO é uma equação ----> Uma equação precisa ter dois membros separados por um sinal =
Assim, você não interpretou corretamente o enunciado:
O inverso de x + 1 ------> 1/(x + 1)
é igual ----> =
x - 1
1/(x + 1) = x - 1 ----> 1 = (x + 1)*(x - 1) -----> 1 = x² - 2x + 1 ----> x² - 2x = 0 ----> x*(x - 2) = 0
Temos duas soluções:
1) x = 0 ----> não serve pois x é positivo
2) x - 2 = 0 ----> x = 2
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por jose henrique » Seg Set 13, 2010 19:21
por jose henrique » Seg Set 13, 2010 19:21
então o gabarito do meu está errado, pois deu
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
 por jose henrique » Sáb Set 18, 2010 22:25
por jose henrique » Sáb Set 18, 2010 22:25
só não entendi de onde surgiu o 2
-
jose henrique
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qui Ago 12, 2010 20:32
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: outros
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação de 2ºgrau
por Anniinha » Dom Out 31, 2010 02:32
- 0 Respostas
- 1174 Exibições
- Última mensagem por Anniinha

Dom Out 31, 2010 02:32
Números Complexos
-
- equação do 2ºgrau
por malcionio » Dom Jun 24, 2012 11:29
- 3 Respostas
- 2368 Exibições
- Última mensagem por e8group

Dom Jun 24, 2012 18:46
Sistemas de Equações
-
- Finalizando uma Eq do 2ºGrau
por leticiamarinho_ » Dom Mar 13, 2011 14:16
- 7 Respostas
- 4118 Exibições
- Última mensagem por LuizAquino

Seg Mar 14, 2011 14:30
Álgebra Elementar
-
- [Funções] Achar a intersecção da parábola 2ºgrau
por thoamas343 » Ter Mar 21, 2017 18:42
- 1 Respostas
- 3085 Exibições
- Última mensagem por petras

Qui Mar 23, 2017 18:28
Funções
-
- Equação - Dúvida básica sobre a proporcionalidade de equação
por FelipeGM » Qui Jan 12, 2012 19:05
- 4 Respostas
- 7731 Exibições
- Última mensagem por FelipeGM

Sáb Jan 14, 2012 13:16
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.





![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)