 por brunotst » Sex Ago 27, 2010 21:11
por brunotst » Sex Ago 27, 2010 21:11
Pessoal, não estou conseguindo resolver esta questão abaixo, por favor me ajudem.
O sistema abaixo será possível e indeterminado somente se:
ax+y=0
2x+3y=0
a) a=2/3
b) a=3
c) a#3
d) a#2/3
e) a=0
-
brunotst
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Dom Ago 01, 2010 12:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Administração
- Andamento: cursando
 por Molina » Sáb Ago 28, 2010 13:17
por Molina » Sáb Ago 28, 2010 13:17
brunotst escreveu:Pessoal, não estou conseguindo resolver esta questão abaixo, por favor me ajudem.
O sistema abaixo será possível e indeterminado somente se:
ax+y=0
2x+3y=0
a) a=2/3
b) a=3
c) a#3
d) a#2/3
e) a=0
Boa dia, Bruno.
Para um sistema ser
possível e indeterminado, temos que satisfazer

,

e
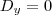
, onde
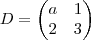


É fácil perceber que o determinante das duas últimas matrizes é igual a 0, pois a segunda coluna é nula. ENtão basta verificar pra que valor de
a na primeira matriz o determinante daria 0.
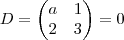


Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Sistemas de Equações
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- SISTEMA DUVIDA
por MatheusFaccioli » Sex Dez 03, 2010 17:18
- 1 Respostas
- 1049 Exibições
- Última mensagem por Molina

Sáb Dez 04, 2010 18:38
Sistemas de Equações
-
- SISTEMA LINEAR DÚVIDA
por Fernanda Lauton » Qui Jun 10, 2010 19:43
- 4 Respostas
- 3330 Exibições
- Última mensagem por MarceloFantini

Sáb Jun 12, 2010 12:37
Sistemas de Equações
-
- Sistema Linear - Dúvida
por Veronica » Seg Abr 23, 2012 22:34
- 0 Respostas
- 1148 Exibições
- Última mensagem por Veronica

Seg Abr 23, 2012 22:34
Sistemas de Equações
-
- [Sistema linear dúvida]
por Aprendiz2012 » Dom Ago 26, 2012 21:26
- 1 Respostas
- 1612 Exibições
- Última mensagem por MarceloFantini

Dom Ago 26, 2012 22:57
Sistemas de Equações
-
- [Sistema] Dúvida exercício
por MrJuniorFerr » Qui Out 11, 2012 23:45
- 1 Respostas
- 1551 Exibições
- Última mensagem por young_jedi

Sex Out 12, 2012 12:27
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 ,
,  e
e 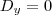 , onde
, onde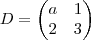


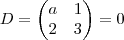



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.