Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por karla_paula » Dom Jun 13, 2010 15:06
por karla_paula » Dom Jun 13, 2010 15:06
41. Sejam:
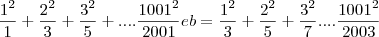
Qual é o inteiro mais próximo de a – b?
(A) 1001.
(B) 500.
(C) 999.
(D) 1000.
(E) 501
-
karla_paula
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Sáb Jun 12, 2010 08:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matematica
- Andamento: formado
 por Vininhuu » Seg Jul 12, 2010 15:51
por Vininhuu » Seg Jul 12, 2010 15:51
O
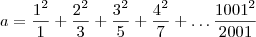
?
É que ali não consta o valor de

, só mostra o "
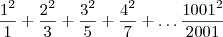
" e o valor de

.
-
Vininhuu
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qui Jun 10, 2010 17:54
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por MarceloFantini » Ter Jul 13, 2010 16:26
por MarceloFantini » Ter Jul 13, 2010 16:26
Quando tivermos 3 parcelas:
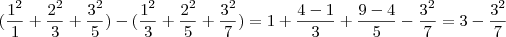
.
Quando tivermos 10 parcelas:


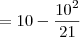
Assim, quando tivermos n parcelas:
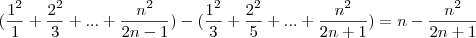
No caso,
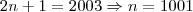
, logo o número inteiro mais próximo é 1001, alternativa A.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Molina » Ter Jul 13, 2010 16:55
por Molina » Ter Jul 13, 2010 16:55
Boa tarde, Karla.
Problema interessante. Se depois puder nos dizer de qual concurso foi, ficaria grato.
Vou reescrever os dados que você passou:
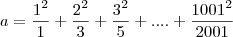
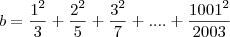
Só que agora vou colocar todas as frações de a e b com o mesmo denominador uma embaixo da outra, para facilitar na visualização da subtração:
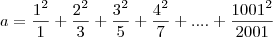
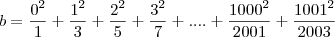
Note que eu não fiz nenhuma alteração, apenas adicionei um termo nulo em b para ficar alinhado os denominadores. Subtraindo

, termo a termo com o mesmo denominador você irá obter:


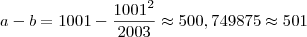
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por MarceloFantini » Ter Jul 13, 2010 16:57
por MarceloFantini » Ter Jul 13, 2010 16:57
Quero pedir desculpas. Errei na hora do resultado final, aqui está o certo:
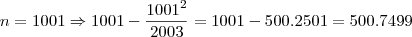
, ou seja, o número inteiro mais próximo é 501, letra E.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Desafios Médios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questões de concurso
por Thaise » Sex Nov 25, 2011 15:12
- 1 Respostas
- 989 Exibições
- Última mensagem por LuizAquino

Sex Nov 25, 2011 16:09
Sistemas de Equações
-
- questoes de esfera
por camilalindynha » Ter Dez 11, 2007 09:12
- 1 Respostas
- 11223 Exibições
- Última mensagem por admin

Ter Dez 11, 2007 12:26
Geometria Espacial
-
- Questões da UFRGS
por Neperiano » Qua Fev 11, 2009 18:32
- 3 Respostas
- 24243 Exibições
- Última mensagem por rcompany

Qui Fev 21, 2019 23:21
Desafios Enviados
-
- resolução de questões
por emerson meneses » Ter Jul 07, 2009 17:28
- 0 Respostas
- 2253 Exibições
- Última mensagem por emerson meneses

Ter Jul 07, 2009 17:28
Geometria Analítica
-
- Questões de matemática
por Erleide » Seg Mar 08, 2010 21:37
- 1 Respostas
- 2223 Exibições
- Última mensagem por MarceloFantini

Seg Mar 08, 2010 22:34
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
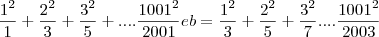

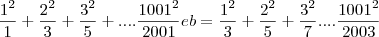

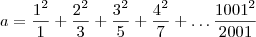 ?
? , só mostra o "
, só mostra o "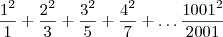 " e o valor de
" e o valor de  .
.
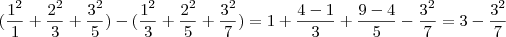 .
.

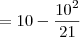
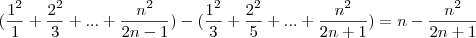
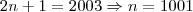 , logo o número inteiro mais próximo é 1001, alternativa A.
, logo o número inteiro mais próximo é 1001, alternativa A.

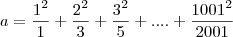
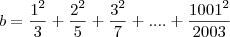
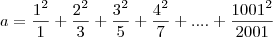
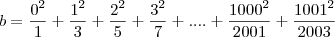
 , termo a termo com o mesmo denominador você irá obter:
, termo a termo com o mesmo denominador você irá obter:

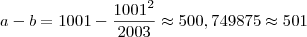


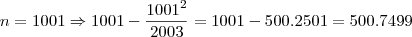 , ou seja, o número inteiro mais próximo é 501, letra E.
, ou seja, o número inteiro mais próximo é 501, letra E.
