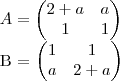
então, a soma dos elementos da diagonal principal de
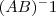 é igual a:
é igual a:gabarito:
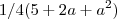
Então, eu achei oq está dentro do parênteses como resposta.. não entendi o porquê do "1/4"
alguém pode fazer pra mim? obrigada

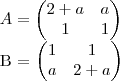
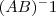 é igual a:
é igual a: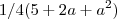

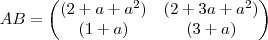
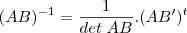
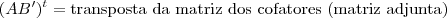
![det AB = (2+a+a^2)\;.\;[(1+a) + 2]\; - \; [(2+a+a^2) + 2a]\;.\;(1+a) = 4+2a+2a^2 - 2a - 2a^2 = 4 det AB = (2+a+a^2)\;.\;[(1+a) + 2]\; - \; [(2+a+a^2) + 2a]\;.\;(1+a) = 4+2a+2a^2 - 2a - 2a^2 = 4](/latexrender/pictures/1956ff42b63d2e9dec41079bf885ec1e.png)
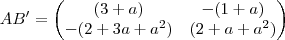
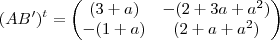
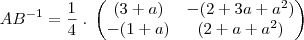
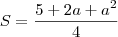



Voltar para Matrizes e Determinantes
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 .
.
 :
: