 por Carolziiinhaaah » Sáb Jun 19, 2010 11:59
por Carolziiinhaaah » Sáb Jun 19, 2010 11:59
Seja P(x) um polinômio de grau 5, com coeficientes reais,
admitindo 2 e i como raízes. Se P(1)P(-1) < 0, então o número
de raízes reais de P(x) pertencentes ao intervalo ]-1, 1[ é:
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
-

Carolziiinhaaah
- Usuário Parceiro

-
- Mensagens: 77
- Registrado em: Sex Mai 28, 2010 14:12
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Douglasm » Sáb Jun 19, 2010 21:25
por Douglasm » Sáb Jun 19, 2010 21:25
Olá Carolziiinhaaah. Para resolver esse problema, basta avaliarmos com bastante atenção os dados que temos:
Se
2 e
i são raízes:
*
-i também é raiz;
*
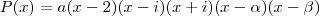
Podemos simplificar isso para:

Fazendo P(1) e P(-1):

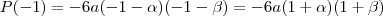
Observando a condição exposta no enunciado:
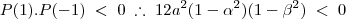
Como

é maior que zero, os outros dois fatores devem possuir sinais opostos. Logo:


Assim demonstramos que só há uma raiz no intervalo ]-1 , 1[ .
Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação com raizes reais
por Thays » Ter Jan 22, 2013 12:48
- 4 Respostas
- 2199 Exibições
- Última mensagem por DanielFerreira

Ter Jan 22, 2013 20:29
Equações
-
- Numero de raízes reais diferentes.
por matheuszila » Dom Nov 28, 2010 14:36
- 6 Respostas
- 3301 Exibições
- Última mensagem por matheuszila

Sex Dez 10, 2010 22:30
Logaritmos
-
- [Equação irracional] Determinação das raízes reais
por Gustavo Gomes » Qui Jan 31, 2013 22:03
- 2 Respostas
- 1367 Exibições
- Última mensagem por Russman

Sex Fev 01, 2013 04:02
Equações
-
- Determinar as raízes de um polinômio
por nanasouza123 » Sex Set 22, 2017 21:09
- 1 Respostas
- 4972 Exibições
- Última mensagem por DanielFerreira

Sex Nov 20, 2020 19:07
Polinômios
-
- zeros reais de funções reais
por bebelo32 » Dom Mar 11, 2018 21:12
- 2 Respostas
- 5507 Exibições
- Última mensagem por adauto martins

Seg Abr 23, 2018 17:52
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



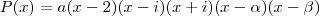


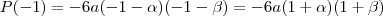
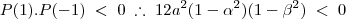
 é maior que zero, os outros dois fatores devem possuir sinais opostos. Logo:
é maior que zero, os outros dois fatores devem possuir sinais opostos. Logo: 



 .
.



