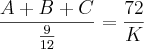
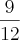 para o segundo membro certo?
para o segundo membro certo?Mas como é que eu passo? multiplico ou divido por
 inverto a fração ou conservo do jeito que está antes de dividir ou de multiplicar? e Porque?
inverto a fração ou conservo do jeito que está antes de dividir ou de multiplicar? e Porque?
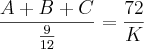
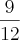 para o segundo membro certo?
para o segundo membro certo? inverto a fração ou conservo do jeito que está antes de dividir ou de multiplicar? e Porque?
inverto a fração ou conservo do jeito que está antes de dividir ou de multiplicar? e Porque?
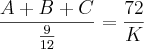
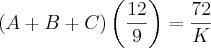



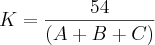


 , se eu fizer
, se eu fizer  e multiplicar
e multiplicar 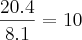 , estará correto.
, estará correto.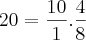 vai dar
vai dar  , e
, e 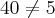 , isso é que está me confundindo :S
, isso é que está me confundindo :S
 (Está correto)
(Está correto)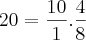




 Pois bem amigos isso é mt simples mas está mais complicado do que eu previ ^^ ainda não consegui chegar numa resposta definitiva:
Pois bem amigos isso é mt simples mas está mais complicado do que eu previ ^^ ainda não consegui chegar numa resposta definitiva: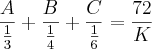
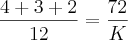
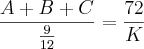
 .
.



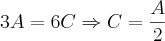

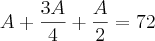



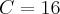



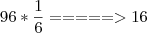
Dividir o número 72 inversamente proporcional aos números 3, 4 e 6
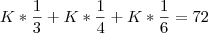



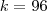







Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante