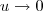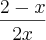por CloudP4 » Seg Jun 07, 2010 23:57
por CloudP4 » Seg Jun 07, 2010 23:57
Olá pessoal, novo aqui no fórum, e em uma lista de exercicios dada pelo meu professor, parei nesses 2 problemas, ainda tenho algumas dúvidas quando ao uso de raíz e do uso de expressões nesse formato

![\lim_{x \rightarrow 3} \frac{\sqrt[]{x} - \sqrt[]{3}}{x-3} \lim_{x \rightarrow 3} \frac{\sqrt[]{x} - \sqrt[]{3}}{x-3}](/latexrender/pictures/b82ac6c9107e592e5873d5251a393b7b.png)
Aos que puderem me explica como pelo menos começar, já agradeço.
Abraços.
-
CloudP4
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Jun 07, 2010 23:45
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng. Civil
- Andamento: cursando
 por Molina » Ter Jun 08, 2010 00:03
por Molina » Ter Jun 08, 2010 00:03
Bem-vindo e boa noite!
Em casos em que o limite dá

ou

podemos usar a Regra de L'Hopital. Mas você só pode usar essa regra depois de ver derivadas. Caso não tenha visto, informe que tentamos por outros meios..
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por CloudP4 » Ter Jun 08, 2010 00:18
por CloudP4 » Ter Jun 08, 2010 00:18
No caso, ainda não vi derivada, limite acho que a quase 2 meses desde que comecei a ver. Ainda não cheguei a Derivada.
O meu caso é que o professor apresentou em seus exemplo algo mais "simples", e não tenho uma base muito boa para esse tipo de exercicio.
-
CloudP4
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Jun 07, 2010 23:45
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng. Civil
- Andamento: cursando
 por Molina » Ter Jun 08, 2010 01:07
por Molina » Ter Jun 08, 2010 01:07
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Molina » Ter Jun 08, 2010 07:59
por Molina » Ter Jun 08, 2010 07:59
Eh verdade. Errei por excesso, hehe! Mas o resultado da o mesmo.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por CloudP4 » Ter Jun 08, 2010 08:52
por CloudP4 » Ter Jun 08, 2010 08:52
Opa muito bom, só não entendi ainda o porque a equação fica desse jeito após "ajustar o númerador", no caso, da onde surgiu esse
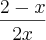
-
CloudP4
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Jun 07, 2010 23:45
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Eng. Civil
- Andamento: cursando
 por MarceloFantini » Dom Jun 13, 2010 19:04
por MarceloFantini » Dom Jun 13, 2010 19:04
É só fazer o mmc.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- exercícios de cálculo 3
 por ezidia51 » Sáb Nov 09, 2019 21:27
por ezidia51 » Sáb Nov 09, 2019 21:27
- 0 Respostas
- 5042 Exibições
- Última mensagem por ezidia51

Sáb Nov 09, 2019 21:27
Cálculo: Limites, Derivadas e Integrais
-
- exercícios de cálculo 3
 por ezidia51 » Sáb Nov 09, 2019 21:32
por ezidia51 » Sáb Nov 09, 2019 21:32
- 1 Respostas
- 3014 Exibições
- Última mensagem por ezidia51

Sáb Nov 09, 2019 21:34
Cálculo: Limites, Derivadas e Integrais
-
- exercícios de cálculo 3
 por ezidia51 » Sáb Nov 09, 2019 21:39
por ezidia51 » Sáb Nov 09, 2019 21:39
- 1 Respostas
- 4172 Exibições
- Última mensagem por adauto martins

Dom Nov 10, 2019 00:29
Cálculo: Limites, Derivadas e Integrais
-
- exercícios de cálculo 3
 por ezidia51 » Dom Nov 10, 2019 15:22
por ezidia51 » Dom Nov 10, 2019 15:22
- 3 Respostas
- 7195 Exibições
- Última mensagem por adauto martins

Dom Nov 10, 2019 21:07
Cálculo: Limites, Derivadas e Integrais
-
- Duvida no exercícios de calculo II
por 1marcus » Dom Abr 26, 2020 16:32
- 2 Respostas
- 5174 Exibições
- Última mensagem por adauto martins

Sáb Mai 02, 2020 14:57
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

![\lim_{x \rightarrow 3} \frac{\sqrt[]{x} - \sqrt[]{3}}{x-3} \lim_{x \rightarrow 3} \frac{\sqrt[]{x} - \sqrt[]{3}}{x-3}](/latexrender/pictures/b82ac6c9107e592e5873d5251a393b7b.png)


![\lim_{x \rightarrow 3} \frac{\sqrt[]{x} - \sqrt[]{3}}{x-3} \lim_{x \rightarrow 3} \frac{\sqrt[]{x} - \sqrt[]{3}}{x-3}](/latexrender/pictures/b82ac6c9107e592e5873d5251a393b7b.png)

 ou
ou  podemos usar a Regra de L'Hopital. Mas você só pode usar essa regra depois de ver derivadas. Caso não tenha visto, informe que tentamos por outros meios..
podemos usar a Regra de L'Hopital. Mas você só pode usar essa regra depois de ver derivadas. Caso não tenha visto, informe que tentamos por outros meios..



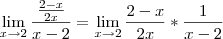
 , com isso
, com isso 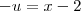 . E quando
. E quando 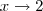 ,
,