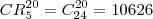Olá Douglas, muito obrigado pela resposta.
Realmente não conhecia a Combinação Completa, segui o seu conselho e comprei um livro de análise combinatória que julguei ser bom (
http://www.siciliano.com.br/produto/264 ... babilidade) e me deparei com exercícios interessantes, onde percebi por exemplo que o problema que citei no ítem "A" poderia ser descrito como a+b+c+d+e = 20 , sendo resolvido realmente utilizando a Combinação Completa.
Porém tive problemas com outros exercícios, vou citá-los:
1) Quantas são as soluções inteiras e não negativas da inequação x + y + z <= 5 ?
Para resolvê-lo, separei em 6 equações e apliquei a Combinação Completa em cada uma:
a) x + y + z = 5
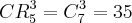
b) x + y + z = 4
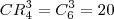
c) x + y + z = 3
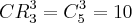
d) x + y + z = 2
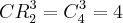
e) x + y + z = 1
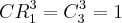
f) x + y + z = 0
Que não dá pra ser aplicado a CR, mas intuitivamente é 1
Sendo assim: 35 + 20 + 10 + 4 + 1 + 1 = 71; Porém o gabarito é 56.
Fiz todas as permutações a mão (acredite) e realmente é 56, e todas as parciais são diferentes das anteriores com exceção da c:
a) 21, b) 15, c) 10, d) 6, e) 3, f)1 -> 56
Tive o mesmo problema em outro exercício:
2) Quantas são as soluções inteiras da equação x + y + z = 20, nas quais nenhuma é menor que 2? Sugestão: chame x = a + 2, y = b + 2 e z = c + 2 e resolva a equação a + b + c = 14.
Solução:

Porém o gabarito é 120.
Onde eu errei na solução destes problemas ?


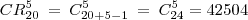
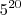 , pois cada elemento é diferente do outro e pode entrar em qualquer uma das 5 caixas. (5 . 5 . 5 . 5 . 5 . 5 . 5 . {...} . 5 - 20 vezes)
, pois cada elemento é diferente do outro e pode entrar em qualquer uma das 5 caixas. (5 . 5 . 5 . 5 . 5 . 5 . 5 . {...} . 5 - 20 vezes)

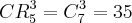
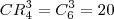
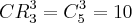
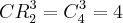
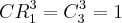



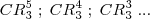




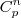 , preferem fazer
, preferem fazer 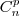 . É interessante tomar muito cuidado com isso, e observar bem que combinação está fazendo.
. É interessante tomar muito cuidado com isso, e observar bem que combinação está fazendo.