 por manuoliveira » Ter Jun 01, 2010 21:02
por manuoliveira » Ter Jun 01, 2010 21:02
(MACK) Em [0, 2?], se

é a maior raiz da equação
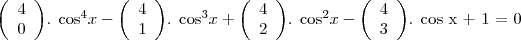
, então sen 3

/4 vale:
Resposta: -1
-
manuoliveira
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qui Abr 01, 2010 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
 por Douglasm » Qua Jun 02, 2010 13:40
por Douglasm » Qua Jun 02, 2010 13:40
Olá Manu. Sendo esse o desenvolvimento do binômio
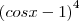
, temos:
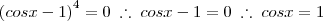
Nessa situação, x poderá assumir 2 valores:

e

. Como

é a maior raiz, ficamos com
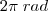
. Deste modo:
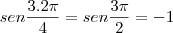
Até a próxima.
-

Douglasm
- Colaborador Voluntário

-
- Mensagens: 270
- Registrado em: Seg Fev 15, 2010 10:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Mathmatematica » Dom Jun 06, 2010 21:22
por Mathmatematica » Dom Jun 06, 2010 21:22
Legal!!! As questões binomiais são mesmo muito interessantes!!!
-
Mathmatematica
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Sex Jun 04, 2010 23:53
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado
- Andamento: cursando
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Mack-SP
por -Sarah- » Sáb Fev 23, 2013 18:56
- 4 Respostas
- 2939 Exibições
- Última mensagem por -Sarah-

Ter Fev 26, 2013 20:20
Funções
-
- mack
 por fna » Qua Jun 12, 2013 08:53
por fna » Qua Jun 12, 2013 08:53
- 0 Respostas
- 935 Exibições
- Última mensagem por fna

Qua Jun 12, 2013 08:53
Geometria Plana
-
- (Mack 98) Circunferência
 por rafaelcb » Qui Set 30, 2010 13:05
por rafaelcb » Qui Set 30, 2010 13:05
- 2 Respostas
- 4782 Exibições
- Última mensagem por rafaelcb

Sex Out 01, 2010 03:17
Geometria Plana
-
- Questão MACK-SP
 por Diego Math » Qui Set 13, 2012 19:11
por Diego Math » Qui Set 13, 2012 19:11
- 2 Respostas
- 8559 Exibições
- Última mensagem por Nina Luizet

Sáb Jun 13, 2015 16:02
Geometria Plana
-
- (MACK-SP) Função do 1º Grau
por 13run0 » Qui Mai 27, 2010 17:54
- 4 Respostas
- 2929 Exibições
- Última mensagem por 13run0

Sex Mai 28, 2010 14:15
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é a maior raiz da equação
é a maior raiz da equação 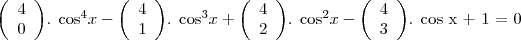 , então sen 3
, então sen 3 /4 vale:
/4 vale:
 é a maior raiz da equação
é a maior raiz da equação 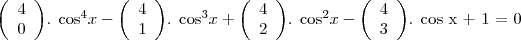 , então sen 3
, então sen 3 /4 vale:
/4 vale:
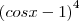 , temos:
, temos: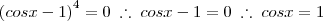
 e
e  . Como
. Como  é a maior raiz, ficamos com
é a maior raiz, ficamos com 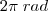 . Deste modo:
. Deste modo: 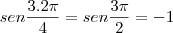



 .
.
 :
: