 por manuoliveira » Sáb Jun 05, 2010 15:29
por manuoliveira » Sáb Jun 05, 2010 15:29
(MACK) Considere a equação

então
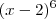
vale:
Resposta: 0
-
manuoliveira
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qui Abr 01, 2010 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
 por Mathmatematica » Dom Jun 06, 2010 21:13
por Mathmatematica » Dom Jun 06, 2010 21:13
Olá Manoel Oliveira! Vamos tentar resolver esse problema.
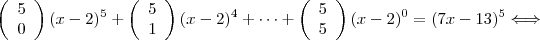
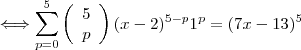
Nós sabemos que
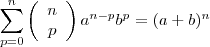
. Então, da equação acima, temos:

Como a potência é ímpar, não precisamos nos preocupar com módulo. Então:
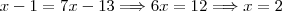
Estamos procurando o valor de
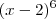
. Substituindo o valor de x encontrado, nessa expressão, temos que
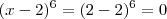
.
Observações:
_Qualquer erro, por favor, AVISEM!!!
-
Mathmatematica
- Usuário Dedicado

-
- Mensagens: 25
- Registrado em: Sex Jun 04, 2010 23:53
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Bacharelado
- Andamento: cursando
Voltar para Binômio de Newton
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Considere a função
por Ana Maria da Silva » Qui Abr 25, 2013 16:06
- 1 Respostas
- 1223 Exibições
- Última mensagem por DanielFerreira

Qui Abr 25, 2013 18:00
Cálculo: Limites, Derivadas e Integrais
-
- Considere que a função w= 33,5+0,6t+(0,45t-35).V^0,15
por Silva339 » Dom Mai 05, 2013 13:06
- 0 Respostas
- 1598 Exibições
- Última mensagem por Silva339

Dom Mai 05, 2013 13:06
Funções
-
- Considere as circunferências...
por David_Estudante » Sáb Mai 25, 2013 17:48
- 0 Respostas
- 789 Exibições
- Última mensagem por David_Estudante

Sáb Mai 25, 2013 17:48
Geometria Analítica
-
- considere as proposiçoes
por flavio neves » Qua Fev 24, 2016 15:10
- 0 Respostas
- 1360 Exibições
- Última mensagem por flavio neves

Qua Fev 24, 2016 15:10
Lógica
-
- (MACK) Em [0, 2?], se...
por manuoliveira » Ter Jun 01, 2010 21:02
- 2 Respostas
- 2679 Exibições
- Última mensagem por Mathmatematica

Dom Jun 06, 2010 21:22
Binômio de Newton
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 então
então 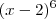 vale:
vale:
 então
então 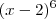 vale:
vale:
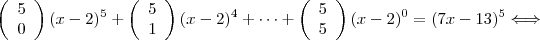
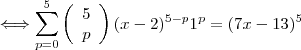
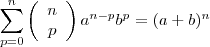 . Então, da equação acima, temos:
. Então, da equação acima, temos:
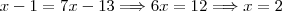
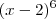 . Substituindo o valor de x encontrado, nessa expressão, temos que
. Substituindo o valor de x encontrado, nessa expressão, temos que 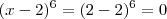 .
.