Como resolver essa equação x2 + x +?(x2 + x + 10) =10 ?
Resp: {-3,2}
Já tentei resolver várias vezes, mas sempre chego numa eq. de 4 grau e não consigo resolver.
Me ajudem, por favor!!!







 , é uma equação do primeiro grau e, portanto, apresenta apenas uma raiz. Ao substituirmos ambos os valores, encontramos que a única raiz é 6. Veja só:
, é uma equação do primeiro grau e, portanto, apresenta apenas uma raiz. Ao substituirmos ambos os valores, encontramos que a única raiz é 6. Veja só: 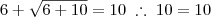

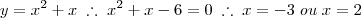

Voltar para Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: