Olá Andymath,
Eu resolveria este problema da seguinte maneira:
Vamos atribuir as notas de cada um dos juízes uma identificação x, y, z e w, de forma que para o participante ser finalista : x + y + z + w >= 22
Vamos resolver esta inequação em 3 partes:
a) x + y + z + w = 22
As possibilidades de notas seriam:
a1) 6 + 6 + 6 + 4
a2) 6 + 6 + 5 + 5
b) x + y + z + w = 23
As possibilidades de notas seriam:
b1) 6 + 6 + 6 + 5
c) x + y + z + w = 24 ( A nota máxima que pode ser obtida 6 + 6 + 6 + 6).
As possibilidades de notas seriam:
c1) 6 + 6 + 6 + 6
Temos ainda que calcular as permutações das 4 possibilidades de notas. Todas elas são permutações com repetição:
a1)
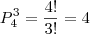
a2)

b1)
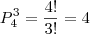
c1)

Total de possibilidades = 4 + 6 + 4 + 1 = 15
Você tem o gabarito para confirmar?
 Encontre o número de maneiras que os juízes têm para atribuir notas de modo que um participante seja finalista.
Encontre o número de maneiras que os juízes têm para atribuir notas de modo que um participante seja finalista.