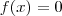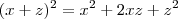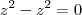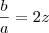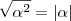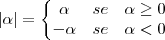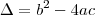Materiais sobre Cálculo.
Utilize a seção de pedidos para outros que não estejam disponíveis.
As fontes dos arquivos serão diversas e deverão ser citadas sempre que possível, mantendo totalmente os créditos dos respectivos autores.
Regras do fórum
- Não envie somente enunciados de problemas, informe suas tentativas e dificuldades!
Queremos que a "ajuda" represente um trabalho interativo, pois saber especificar a dúvida exige estudo.
Serão desconsiderados tópicos apenas com enunciados, sem interação. Nosso objetivo não é resolver listas de exercícios;
- Para não haver má interpretação em suas postagens, especialmente na precedência das operações, utilize LaTeX, podendo ser a partir do botão "editor de fórmulas".
Bons estudos!
 por admin » Qui Mai 15, 2008 15:44
por admin » Qui Mai 15, 2008 15:44
Sendo

uma função do segundo grau, temos:
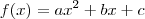
Com

e

.
O objetivo é encontrar uma expressão que determine as raízes desta função.
Ou seja, quais os valores para

onde:
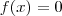
Portanto, o que de fato buscamos é "isolar" x nesta equação:

Vamos dividir por

os dois membros da equação.
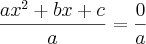
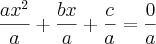


Agora, subtrairemos

:


Antes de prosseguir, lembre-se de um quadrado perfeito, onde:

Proveniente da propriedade distributiva
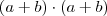
.
Vamos "criar" um quadrado perfeito no primeiro membro da equação.
Para facilitar a visualização, vamos reescrever o quadrado perfeito com outras letras:
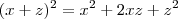
Se chamarmos
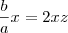
, assim:

Podemos somar e em seguida subtrair

, sem alterarmos a equação, pois
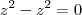

De modo que assim podemos destacar um quadrado perfeito:

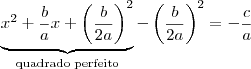
Com o quadrado perfeito visualizado, vamos reescrever a equação:

Somando
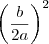
nos dois membros:

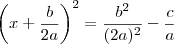

Deixando o segundo membro com o mesmo denominador (m.m.c.):

Extraindo a raiz quadrada dos dois membros:
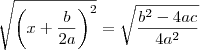
Aqui, cuidado, note que:
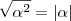
Pois como
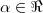
está elevado ao quadrado e a raiz deve ser positiva, eis o papel do módulo: garantir que o resultado da raiz seja positivo, mesmo que

seja negativo.
Lembrando a definição de módulo:
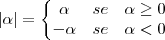
Veja em um exemplo o papel e importância do módulo, com


De fato, pois:

Veja o que aconteceria se não utilizássemos o módulo:
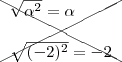
Não deve ocorrer no conjunto dos números reais.
Após estas observações, vamos utilizar módulo na simplificação da raiz:
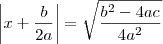
Separando as raízes do segundo membro, numerador e denominador:

Extraindo a raiz do denominador e novamente, o módulo aparece:

Igualmente, também podemos escrever assim:
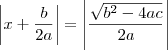
E pela definição de módulo:

Subtraindo
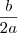
dos dois membros:

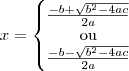
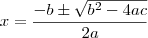
(fórmula de Bhaskara)
Como nos reais o radicando desta raiz

deve sempre ser positivo, ele é freqüentemente avaliado (estudo de sinal), chamado de discriminante (Delta):
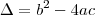
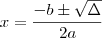
Portanto, as raízes de uma função do segundo grau
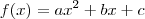
, são obtidas pela expressão:
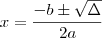
Sendo que:
Se
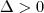
, as duas raízes são reais e distintas;
Se

, há um par de raízes reais e iguais;
Se
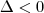
, há um par de raízes complexas.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Cálculo
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Dedução de formula
por rodrigosoaresd » Ter Ago 14, 2012 14:30
- 1 Respostas
- 1693 Exibições
- Última mensagem por e8group

Ter Ago 14, 2012 15:34
Geometria Analítica
-
- Dedução de fórmula física
por useredu » Sex Set 02, 2016 11:55
- 2 Respostas
- 2026 Exibições
- Última mensagem por useredu

Qui Set 08, 2016 13:47
Equações
-
- Bhaskara
por Neperiano » Sex Out 31, 2008 20:57
- 1 Respostas
- 8945 Exibições
- Última mensagem por Tsmmakika

Sáb Set 12, 2015 05:18
Mensagens Matemáticas
-
- [artigo] círculo unitário e algumas relações trigonométricas
 por admin » Ter Jun 03, 2008 17:03
por admin » Ter Jun 03, 2008 17:03
- 1 Respostas
- 2976 Exibições
- Última mensagem por Neperiano

Sex Set 16, 2011 19:48
Geometria
-
- [Equação do 2º grau] Ajuda com resolução de bhaskara
por Everton_Win » Ter Mar 26, 2013 18:36
- 2 Respostas
- 2127 Exibições
- Última mensagem por Everton_Win

Ter Mar 26, 2013 22:50
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 uma função do segundo grau, temos:
uma função do segundo grau, temos: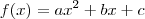
 e
e  .
.onde:

os dois membros da equação.
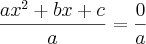
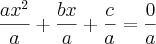


:


.
, assim:

, sem alterarmos a equação, pois


, lembrando que:
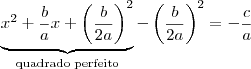

nos dois membros:

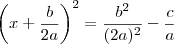


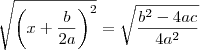
está elevado ao quadrado e a raiz deve ser positiva, eis o papel do módulo: garantir que o resultado da raiz seja positivo, mesmo que
seja negativo.
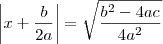


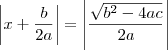

dos dois membros:

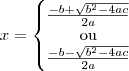
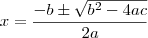
deve sempre ser positivo, ele é freqüentemente avaliado (estudo de sinal), chamado de discriminante (Delta):
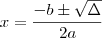
, são obtidas pela expressão:
, as duas raízes são reais e distintas;
, há um par de raízes reais e iguais;
, há um par de raízes complexas.