por cortesfsa » Seg Mar 29, 2010 10:31
Olá pessoal! Aqui vai uma questão cabeluda:
Tendo em vista as relações descritas na figura ao lado calcular as distâncias x e y.
Abraços :wink:
- Anexos
-
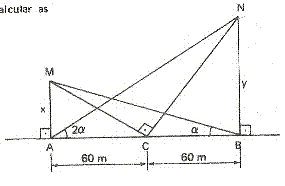
- questão.GIF (4.07 KiB) Exibido 2129 vezes
Editado pela última vez por
cortesfsa em Seg Mar 29, 2010 20:09, em um total de 1 vez.
Bronze OBQ Norte/Nordeste
---
"Try not. Do, or do not. There is no try." --Yoda
"Computer, compute to the last digit the value of pi" --Spock
"I have a bad feeling about this..." --Obi-Wan
-
cortesfsa
- Novo Usuário
-
- Mensagens: 4
- Registrado em: Sex Dez 18, 2009 22:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
por cortesfsa » Seg Mar 29, 2010 20:04
Duvido que alguem consiga
Bronze OBQ Norte/Nordeste
---
"Try not. Do, or do not. There is no try." --Yoda
"Computer, compute to the last digit the value of pi" --Spock
"I have a bad feeling about this..." --Obi-Wan
-
cortesfsa
- Novo Usuário
-
- Mensagens: 4
- Registrado em: Sex Dez 18, 2009 22:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
por Elcioschin » Seg Mar 29, 2010 20:30
Duvida mesmo cortesfsa ?
Aliás nem é um problema tão "cabeludo" assim: na verdade o problema é "careca" e usa peruca!!!
Seja b = ângulo NCB seja a = alfa
Triângulos NCB e CMA são semelhantes ----> ângulo NCB = ângulo CMA = b
tgb = 60/x = y/60 -----> xy = 3600 ----> y = 3600/x ---->I
tga = x/120 ----> II
tg(2a) = y/120 -----> 2*tga/(1 - tg²a) = y/120 -----> 2*(x/120)/[1 - (x/120)²] = (3600/x)/120 ----> x*(x/60) = 30*[(14400 - x²)/14400] ----> x² = (14400 - x²)/8 ---->
9x² = 14400 ----> x² = 1600 ----> x = 40 ----> y = 90
-
Elcioschin
- Colaborador Voluntário
-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Progressao] série geometrica X progressao geometrica?
por aajunim » Seg Mar 18, 2013 11:19
- 2 Respostas
- 4095 Exibições
- Última mensagem por aajunim
Ter Mar 19, 2013 11:44
Progressões
-
- [trigonometria] trigonometria em triangulo qualquer
por biamassa00 » Sex Mai 25, 2012 22:19
- 0 Respostas
- 3497 Exibições
- Última mensagem por biamassa00
Sex Mai 25, 2012 22:19
Trigonometria
-
- Geometrica
por Misao » Qui Jun 18, 2009 12:42
- 1 Respostas
- 1369 Exibições
- Última mensagem por Molina
Qui Jun 18, 2009 14:00
Progressões
-
- Progressão geométrica (ITA)
por Ananda » Sex Mar 07, 2008 13:27
- 17 Respostas
- 25032 Exibições
- Última mensagem por Ananda
Qui Mar 13, 2008 11:10
Progressões
-
- Progressão Geométrica
por nicecaps » Seg Mar 22, 2010 11:37
- 2 Respostas
- 4112 Exibições
- Última mensagem por nicecaps
Ter Mar 23, 2010 09:45
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
