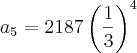por TEKA » Qui Mar 25, 2010 18:48
por TEKA » Qui Mar 25, 2010 18:48
ola
queria saber a parte teórica da pa e da pg. vcs conhecem algum site que possa pegar?
ou senão me ajudar em como resolver, uma pg, simples, pois ele dá a sequencia....2187, 729 243 e 81.
o próximo termo é?....
não me recordo a fórmula, nem se é an= a1.q n-1...onde o an é 4, ou é o 5 elemento?
a1 seria o 2187?
desculpe mas é que já faz tempo que estudei e to tentando ou vestibular......
valew
-
TEKA
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Mar 25, 2010 18:24
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: g projetos
- Andamento: formado
 por Cleyson007 » Qui Mar 25, 2010 19:40
por Cleyson007 » Qui Mar 25, 2010 19:40
Boa noite Teka!
Vão algumas dicas:
Fórmula do termo geral:
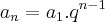
Teka, o

é o quinto termo que você procura.
O número 2187 é o primeiro termo

A letra q é a razão dessa P.G

Note que o valor de q é um termo dividido por quem o antecede.
A letra n é o número de termos, logo:

Agora, ficou mais fácil! Tente você mesma resolver

Comente qualquer dúvida.
Link para conferir mais sobre a matéria:
http://www.brasilescola.com/matematica/ ... etrica.htmAté mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por TEKA » Qui Mar 25, 2010 19:51
por TEKA » Qui Mar 25, 2010 19:51
OBRIGADAAAO MESMO.
EU fiz assim,
a5 = a4.q
o q = [a2/a1] = no caso deu 1/3
a4 = 81
ai substitui na fórmula a5 = 81x1/3 = 27
super obrigada mesmo assim.
-
TEKA
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qui Mar 25, 2010 18:24
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: g projetos
- Andamento: formado
 por Cleyson007 » Qui Mar 25, 2010 20:03
por Cleyson007 » Qui Mar 25, 2010 20:03
Boa noite Teka!
É isso mesmo!
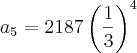
Resolvendo,

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda para resolver equação para calcular velocidade média
por marcorrer » Sex Fev 24, 2012 13:10
- 0 Respostas
- 3701 Exibições
- Última mensagem por marcorrer

Sex Fev 24, 2012 13:10
Sistemas de Equações
-
- onde a funcao tem concavidade para cima e para baixo?
por tumiattibrz » Sáb Jun 04, 2011 01:00
- 4 Respostas
- 4671 Exibições
- Última mensagem por Fabio Cabral

Seg Jun 06, 2011 23:54
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Funciona para produto mas não para quociente?
por Matheus Lacombe O » Ter Dez 11, 2012 23:46
- 1 Respostas
- 2189 Exibições
- Última mensagem por Russman

Qua Dez 12, 2012 01:39
Cálculo: Limites, Derivadas e Integrais
-
- teoria de conjunto
por rafaelmtmtc » Sáb Abr 18, 2009 20:45
- 4 Respostas
- 3349 Exibições
- Última mensagem por rafaelmtmtc

Dom Abr 19, 2009 12:47
Equações
-
- (ESTATÍSTICA ) Teoria
 por Roberta » Ter Ago 11, 2009 23:18
por Roberta » Ter Ago 11, 2009 23:18
- 4 Respostas
- 4931 Exibições
- Última mensagem por Roberta

Qui Ago 13, 2009 15:40
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


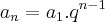
 é o quinto termo que você procura.
é o quinto termo que você procura.