Provavelmente deve haver uma forma mais simples de resolver, no entanto, abaixo segue a minha resolução.
Estas "comissões" podem ser feitas de 3 formas diferentes havendo ao menos 3 homens nelas:
1ª) Apenas 3 homens: Comissão formada por 3 homens e 2 mulheres. Teremos portanto um numero de comissões igual a
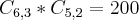
2ª) 4 Homens: Comissão formada por 4 homens e 1 mulheres. Teremos portanto um numero de comissões igual a

3ª) 5 Homens: Comissão formada por 5 homens e nenhuma mulhere. Teremos portanto um numero de comissões igual a
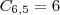
O numero total de comissões é igual a soma destas tres possibilidades: 200 + 75 + 6 = 281 grupos diferentes (letra B)
Note que a forma que tu utilizou é apenas uma das possiveis formas de montar o grupo.
Espero ter ajudado, bons estudos.


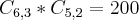

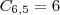



 .
.
 :
: