Nesta eu igualei o ln(2x+1) a "y", fiz a fórmula resolvente e obtive os dois zeros: -1 e -2.
A minha dúvida está em como apresento o resultado final tendo estes resultados.
Nesta ainda não fiz nada e precisava de ajuda :s
Agradecia imenso uma ajuda , com os passos se possível..
Muito obrigado,
Cumprimentos.
![x>-1/2\rightarrow (-\frac{1}{2};\frac{1-{e}^{2}}{2{e}^{2}}]](/latexrender/pictures/59b6ee6524dbc08914ed312f4ecaf3e0.png "x>-1/2\rightarrow (-\frac{1}{2};\frac{1-{e}^{2}}{2{e}^{2}}]")
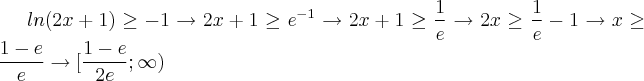
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)