 por Gabiejonas1212 » Qui Nov 17, 2016 17:28
por Gabiejonas1212 » Qui Nov 17, 2016 17:28
Boa tarde, já tentei resolver mas só consigo colocar na fórmula do quociente e não sei dar continuidade, por favor me ajudem.
F (x)'= 2x/(x^2)
-
Gabiejonas1212
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Nov 17, 2016 17:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Qui Nov 17, 2016 18:31
por Cleyson007 » Qui Nov 17, 2016 18:31
Olá, boa tarde!
Desejo-lhe as boas vindas

Não entendi a sua pergunta.. Você quer saber como derivo a função
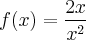
utilizando a Regra do Quociente?
Abraço
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Gabiejonas1212 » Dom Nov 20, 2016 13:33
por Gabiejonas1212 » Dom Nov 20, 2016 13:33
Sim está é a minha dúvida, obrigada pelas boas vindas!
-
Gabiejonas1212
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Nov 17, 2016 17:19
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Cleyson007 » Dom Nov 20, 2016 16:30
por Cleyson007 » Dom Nov 20, 2016 16:30
Olá, boa tarde!
É um prazer ajudar..
Vamos lá!
Repare que
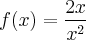
é uma função racional (escrita numa forma de fração P(x)/Q(x)). Repare ainda que P(x) e Q(x) são funções polinomiais e, portanto, contínuas em IR.
Aqui, vamos então aplicar a Regra do Quociente para derivação.
https://ap.imagensbrasil.org/images/201 ... ciente.pngA Regra do Quociente funciona da seguinte forma: [Pego a derivada do numerador e multiplico pelo denominador; subtrai da derivada do denominador multiplicada pelo numerador] / (denominador)²
Assim sendo, f ' (x) = [2*(x²) - 2x*(2x)] / [(x²)²]
f ' (x) = [2x² - 4x²] / x^4
f ' (x) = -2 / x²
Sou formado em Matemática e tenho um trabalho muito bacana para estudantes com dificuldade. Anote o meu WhatsApp caso tenha interesse, por favor: (38) 99889-5755.
Qualquer coisa me mande uma mensagem que lhe explico direitinho como funciona.
Abraço,
Prof. Clésio
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ajuda
por Daiane kelly » Seg Mar 24, 2008 22:38
- 4 Respostas
- 6119 Exibições
- Última mensagem por Cleyson007

Ter Mai 12, 2009 17:43
Matrizes e Determinantes
-
- Ajuda
por Umbus » Sáb Out 18, 2008 14:12
- 2 Respostas
- 3475 Exibições
- Última mensagem por lopes

Sáb Jun 20, 2009 15:51
Álgebra Linear
-
- Ajuda.
por VanessaFontela » Qui Dez 04, 2008 10:32
- 0 Respostas
- 2767 Exibições
- Última mensagem por VanessaFontela

Qui Dez 04, 2008 10:32
Matemática Financeira
-
- Ajuda!!!
por GABRIELA » Seg Set 21, 2009 17:28
- 1 Respostas
- 2141 Exibições
- Última mensagem por Molina

Seg Set 21, 2009 19:56
Sistemas de Equações
-
- Ajuda!!!!!!
por GABRIELA » Ter Set 22, 2009 16:35
- 6 Respostas
- 4107 Exibições
- Última mensagem por GABRIELA

Qui Set 24, 2009 16:29
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




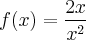 utilizando a Regra do Quociente?
utilizando a Regra do Quociente?

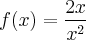 é uma função racional (escrita numa forma de fração P(x)/Q(x)). Repare ainda que P(x) e Q(x) são funções polinomiais e, portanto, contínuas em IR.
é uma função racional (escrita numa forma de fração P(x)/Q(x)). Repare ainda que P(x) e Q(x) são funções polinomiais e, portanto, contínuas em IR.





