A grande demanda de um novo modelo de equipamento digital provocou inicialmente um aumento em seu preço de mercado. No
entanto, depois de algum tempo, o lançamento por outros fabricantes de aparelhos similares, provocou uma queda nesses preços.
Observando?se a variação no preço, ano a ano, concluiu-se que ele poderia ser modelado através da função f(x)=2000.5^(2x-x²)/4, em que f(0) representa o preço de mercado no ano de lançamento do aparelho e f(x), para x > 0, representa o preço de mercado, x anos
após o lançamento do aparelho.
Sabendo que a partir de determinado ano t o preço do referido aparelho será inferior à metade do preço de lançamento e considerando
log 2 = 0,3, determine o valor de t.




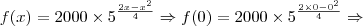

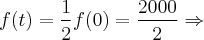


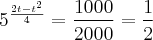




![\sqrt[]{\Delta} = \sqrt[]{b^2 - 4ac} \Rightarrow \sqrt[]{\Delta} = \sqrt[]{4 + 6,84} \Rightarrow \sqrt[]{\Delta} = 3,29 \sqrt[]{\Delta} = \sqrt[]{b^2 - 4ac} \Rightarrow \sqrt[]{\Delta} = \sqrt[]{4 + 6,84} \Rightarrow \sqrt[]{\Delta} = 3,29](/latexrender/pictures/f6a4b628e8a8bb5e7383335925a35761.png)
![\Rightarrow t = \frac{-b \pm \sqrt[]{\Delta}}{2a} \Rightarrow t = \frac{-2 \pm 3,29}{-2} \Rightarrow \Rightarrow t = \frac{-b \pm \sqrt[]{\Delta}}{2a} \Rightarrow t = \frac{-2 \pm 3,29}{-2} \Rightarrow](/latexrender/pictures/17ef82dff59ef14c1bc7284d4a92d38e.png)


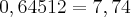
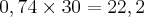


 .
.



