 por Cleyson007 » Sex Jan 22, 2010 18:35
por Cleyson007 » Sex Jan 22, 2010 18:35
Boa tarde!
Estou bastante confuso com a resolução da questão abaixo. Alguém pode me ajudar?
Determine, usando as propriedades da divisão:
O polinômio mônico

de grau 5, tal que
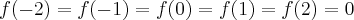
Agradeço sua ajuda.
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Elcioschin » Sex Jan 22, 2010 23:08
por Elcioschin » Sex Jan 22, 2010 23:08
Polinômio mônico é aquele em que o coeficiente do termo de maior grau vale 1:
F(x) = x^5 + ax^4 + bx³ + cx² + dx + e
Para x = 0 ----> F(0) = e ----> 0 = e -----> e = 0
Para x = 1 -----> F(1) = 1 + a + b + c + d ------> a + b + c + d + 1 = 0
Para x = -1 ----> F(-1) = - 1 + a - b + c - d ----> a - b + c - d - 1 = 0
Somando ambas as equações ----> 2a + 2c = 0 ----> c = - a
Para x = 2 -----> F(2) = 32 + 16a + 8b + 4c + 2d ------> 8a + 4b + 2c + d + 16 = 0
Para x = -2 ----> F(-2) = - 32 + 16a - 8b + 4c - 2d ----> 8a - 4b + 2c - d - 16 = 0
Somando ambas ----> 16a + 4c = 0 -----> c = - 4a
Só é possivel para a = 0 e c = 0
Não dá para calcular b, d ---> Só temos ----> b + d = - 1
F(x) = x^5 + bx³ + dx com b + d + 1 = 0 ----> Só conseguí chegar até aqui.
-
Elcioschin
- Colaborador Voluntário

-
- Mensagens: 624
- Registrado em: Sáb Ago 01, 2009 10:49
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: formado
 por MarceloFantini » Sáb Jan 23, 2010 21:59
por MarceloFantini » Sáb Jan 23, 2010 21:59
Boa noite.
Mesmo que

e

sejam desconhecidos, a função ainda é:
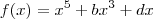
Certo? Ainda não valem as relações
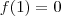
e

? Porque substituindo e resolvendo, encontrei

e

.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por DENILSON RODRIGUES » Seg Fev 16, 2015 20:38
por DENILSON RODRIGUES » Seg Fev 16, 2015 20:38
Boa noite,
Resolvi da seguinte maneira,
Para cada raiz descrita temos um termo (x-a) ou (x+a)que ira formar o polinômio, tal como : f(0) um termo "x" ; para f(1) um termo (x-1); para f(-1) um termo (x+1);
para f(2) m termo (x-2); para f(-2) um termo (x+2). Ao multiplicar todos os termos encontrados, temos:
(x)(x-1)(x+1)(x-2)(x+2)=0
(x^2 + 3x + 2)(x)(x^2 - 3x + 2)=0
(x^3 + 3x^2 + 2x)(x^2 - 3x + 2)=0
* (x^3)(x^2 - 3x + 2) = ( x^5 - 3x^4 + 2x^3 )
* (3x^2)(x^2 - 3x + 2) = ( + 3x^4 - 9x^3 + 6x )
* (2x)(x^2 - 3x + 2) = ( +2x^3 - 6x^2 + 4x )
+__________________________
x^5 + 0 - 5x^3 + 0 + 4x
logo: x^5 -5x^3 +4x é um polinômio mônico(o líder x^5 tem incógnita= 1) e suas raízes são:
f(0) => (0)(x-1)(x+1)(x-2)(x+2)= 0
f(-1)=> (x)(x-1)(-1+1)(x-2)(x+2)= (x)(x-1)(0)(x-2)(x+2)= 0
f(1) => (x)(1-1)(x+1)(x-2)(x+2)= (x)(0)(x+1)(x-2)(x+2)= 0
f(2) => (x)(x-1)(x+1)(2-2)(x+2)= (x)(x-1)(x+1)(0)(x+2)= 0
f(-2)=> (x)(x-1)(x+1)(x-2)(-2+2)= (x)(x-1)(x+1)(x-2)(0)= 0
Espero ter ajudado.
-
DENILSON RODRIGUES
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Fev 16, 2015 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Progressões
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [polinômio]Relações de Girard + raízes de polinômio
por matano2104 » Qui Set 05, 2013 17:02
- 1 Respostas
- 7154 Exibições
- Última mensagem por young_jedi

Qui Set 05, 2013 17:57
Polinômios
-
- Polinômio
por Cleyson007 » Qua Mai 13, 2009 15:18
- 3 Respostas
- 3825 Exibições
- Última mensagem por Molina

Sex Mai 15, 2009 06:46
Polinômios
-
- Polinômio
por Cleyson007 » Qua Jul 15, 2009 23:17
- 3 Respostas
- 2456 Exibições
- Última mensagem por DanielFerreira

Ter Set 22, 2009 12:06
Polinômios
-
- polinomio
por Carolina0991 » Qui Jan 28, 2010 12:50
- 2 Respostas
- 2388 Exibições
- Última mensagem por MarceloFantini

Qui Jan 28, 2010 14:41
Polinômios
-
- polinomio
por Carolina0991 » Qui Jan 28, 2010 21:09
- 1 Respostas
- 1673 Exibições
- Última mensagem por Elcioschin

Qui Jan 28, 2010 22:42
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 de grau 5, tal que
de grau 5, tal que 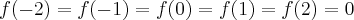

 de grau 5, tal que
de grau 5, tal que 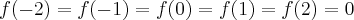


 e
e  sejam desconhecidos, a função ainda é:
sejam desconhecidos, a função ainda é: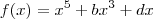
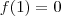 e
e  ? Porque substituindo e resolvendo, encontrei
? Porque substituindo e resolvendo, encontrei  e
e  .
.




 , avisa que eu resolvo.
, avisa que eu resolvo.

