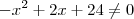por Luiz C » Sex Jan 08, 2010 15:07
por Luiz C » Sex Jan 08, 2010 15:07
A soma S de todos os valores inteiros de x que pertencem ao domínio da função f: R -> R definida por
![f(x)\sqrt[2]{\frac{5}{24 + 2x - x ²}} f(x)\sqrt[2]{\frac{5}{24 + 2x - x ²}}](/latexrender/pictures/04eed3c4e94e29448520020e076a24d8.png)
é igual a :
A. 15
B. 11
C. 9
D. 6
Tentativa
x²-2x-24

0
resolvendo: x'= 6
x''= -4
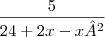

0
Claro isso foi uma tentaviva. A resposta é letra C (9)
Obrigado!
Obs: esse A deve ser desconsiderado e apenas x elevado ao quadrado
-
Luiz C
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Ter Jan 06, 2009 18:40
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Eletroeletronica
- Andamento: formado
 por MarceloFantini » Sex Jan 08, 2010 17:43
por MarceloFantini » Sex Jan 08, 2010 17:43
Boa tarde Luiz!
Você já encontrou as raízes da equação, mas eu plotei um pequeno gráfico da função
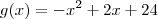
. Afinal, ela é quem delimita toda a função

, uma vez que a função

não pode ser menor que ou igual a zero (estamos trabalhando no conjunto dos números reais, e não podemos dividir por zero).

Basta somar os valores inteiros nesse intervalo:

.
Espero ter ajudado.
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Molina » Sex Jan 08, 2010 20:09
por Molina » Sex Jan 08, 2010 20:09
Boa noite,
Basicamente temos que satisfazer duas condições:
i)
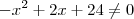
ii)

Unindo as duas condições chegamos a uma definitiva:

Analisando o gráfico...
Podemos ver que ela será positiva no intervalo descrito por Fantini (-4,6).
(Note que é um intervalo aberto, ou seja, não incluimos -4 e nem 6)Somando os números chegamos ao resultado igual ao gabarito: 9.
Bom estudo,

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Função 2º grau] Minha resposta está certa?
por Richard Oliveira » Sex Mai 04, 2012 03:05
- 1 Respostas
- 1720 Exibições
- Última mensagem por MarceloFantini

Sáb Mai 05, 2012 00:06
Funções
-
- tentativa
por Jhennyfer » Dom Ago 18, 2013 12:07
- 4 Respostas
- 2353 Exibições
- Última mensagem por Jhennyfer

Ter Ago 20, 2013 19:06
Logaritmos
-
- Última tentativa frustrada de hj - logaritmo
por Fernanda Lauton » Seg Jun 28, 2010 16:16
- 2 Respostas
- 1559 Exibições
- Última mensagem por Fernanda Lauton

Seg Jun 28, 2010 19:30
Logaritmos
-
- Exercicos da minha apostila
por Guilherme35 » Qui Set 20, 2012 15:11
- 1 Respostas
- 2910 Exibições
- Última mensagem por LuizAquino

Qui Set 20, 2012 15:52
Logaritmos
-
- Ajuda na minha lição
por gahzurc » Qua Abr 23, 2014 18:11
- 0 Respostas
- 948 Exibições
- Última mensagem por gahzurc

Qua Abr 23, 2014 18:11
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x)\sqrt[2]{\frac{5}{24 + 2x - x ²}} f(x)\sqrt[2]{\frac{5}{24 + 2x - x ²}}](/latexrender/pictures/04eed3c4e94e29448520020e076a24d8.png) é igual a :
é igual a : 0
0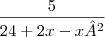
 0
0
![f(x)\sqrt[2]{\frac{5}{24 + 2x - x ²}} f(x)\sqrt[2]{\frac{5}{24 + 2x - x ²}}](/latexrender/pictures/04eed3c4e94e29448520020e076a24d8.png) é igual a :
é igual a : 0
0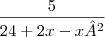
 0
0
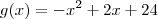 . Afinal, ela é quem delimita toda a função
. Afinal, ela é quem delimita toda a função  , uma vez que a função
, uma vez que a função  não pode ser menor que ou igual a zero (estamos trabalhando no conjunto dos números reais, e não podemos dividir por zero).
não pode ser menor que ou igual a zero (estamos trabalhando no conjunto dos números reais, e não podemos dividir por zero). .
.