- Simetria
1)
 diz-se simétrica se, e somente se, quando
diz-se simétrica se, e somente se, quando  . Isto é:
. Isto é:
Uma relação
 sobre um conjunto A não é simétrica se existirem a e b em A,
sobre um conjunto A não é simétrica se existirem a e b em A,  , tais que
, tais que 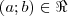 e
e  .
.Até encima tudo bem...
- Transitividade
2)
 diz-se transitiva se, e somente se, quando
diz-se transitiva se, e somente se, quando 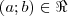 e
e  , então
, então 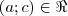 .Isto é:
.Isto é: e
e 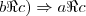
Aqui vem uma dúvida:
Mas neste exemplo:
a) Seja
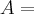 {
{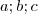 }. A relação sobre A:
}. A relação sobre A: {
{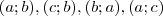 }
}Diz que não é transitiva, pois
 e
e 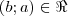 , mas
, mas 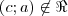 .
.DÚVIDA 01 (a): Mas
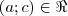 ,
,  , então
, então 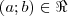 , portanto é transitiva, estou certo?
, portanto é transitiva, estou certo?- Antissimetria
3)
 diz-se antissimétrica se, e somente se, quando (a; b)
diz-se antissimétrica se, e somente se, quando (a; b) 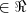 e (b; a)
e (b; a) 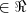 , então, a = b. Isto é:
, então, a = b. Isto é: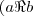 e
e 
Mas neste exemplo:
b) Seja
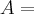 {
{ }. A relação sobre A.
}. A relação sobre A. {
{ }
}não é antissimétrica, pois (4; 2)
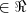 e também (2; 4)
e também (2; 4) 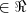 .
.DÚVIDA 02 (b): Eu entendi o exemplo "b)", pois com os elementos (4; 2) e (2; 4) a relação é obviamente simétrica, porém, o que eu não entendo é a definição dado pelo livro sobre a Antissimetria, que diz que
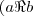 e
e  . Eu não entendo quando ele diz que a = b, embora num exemplo envolvendo "conjunto de conjuntos" eu tenha entendido perfeitamente.
. Eu não entendo quando ele diz que a = b, embora num exemplo envolvendo "conjunto de conjuntos" eu tenha entendido perfeitamente.Agradeço desde já!



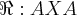 tal q.
tal q.  ={(a,b),(c,b),(b,a),(a,c)}...aqui
={(a,b),(c,b),(b,a),(a,c)}...aqui  ={(a,a),(a,b),(a,c),(b,b),(b,a),(b,c),(c,a),(c,b),(c,c)},pela a definiçao de
={(a,a),(a,b),(a,c),(b,b),(b,a),(b,c),(c,a),(c,b),(c,c)},pela a definiçao de 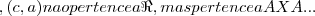 ,logo a relaçao de transitividade em
,logo a relaçao de transitividade em 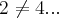

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)