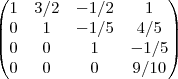por Raffz » Seg Nov 24, 2014 02:23
por Raffz » Seg Nov 24, 2014 02:23
Bom, sou novo aqui no fórum e já começo com uma dúvida, sinto por imcomodar-vos.
Pois bem:
A questão pede para eu dizer se o vetor abaixo pertence a W = [(2,1,0,3), (3,-1,5,2), (-1,0,2,1)]
O vetor é v = (2,3,-7,3)
Eu fiz a relaçao v = aW1+bW2+W3 (onde Wn são os vetores de W, enfim, fiz a relação de combinação linear)
Dai obtive a matriz ampliada que escalonei e me deu a seguinte situação:
1 0 0 -12/5
0 1 0 -1
0 0 1 -1
0 0 0 0
Ai entra a dúvida:
Substituindo o que encontrei em a,b e c não dá o vetor v! Mas como isso se isso foi exatamente o que a matriz me desvendou?
Ou eu fiz tudo errado... Ou eu fiz tudo errado rs
Então agradeceria muito quem me ajudasse nessa questão.
Ps: Estou usando o fórum no celular, por curiosidade, é possível usar o sistema Latex para colocar as fórmulas bonitinhas pelo celular? Ou só na versão desktop?
Abs.
-
Raffz
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Nov 24, 2014 02:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
 por adauto martins » Seg Nov 24, 2014 13:47
por adauto martins » Seg Nov 24, 2014 13:47
se v e vetor de W, entao existem a,b,c reais tal q.
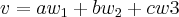
...
![(2,3,-7,3)=a(2,1,0,3)+b(3,-1,5,2)+c(-1,0,2,1)...[tex]\Rightarrow 2a+3b-c=2,a-b=3,5b+2c=-7,3a+2b+c=3... (2,3,-7,3)=a(2,1,0,3)+b(3,-1,5,2)+c(-1,0,2,1)...[tex]\Rightarrow 2a+3b-c=2,a-b=3,5b+2c=-7,3a+2b+c=3...](/latexrender/pictures/94a2085d4d392bfa25ac50f419bc620b.png)
sao as equaçoes,colocando-as em uma matriz completa ...
A=
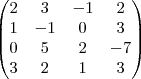
,escalonandom,teremos
...
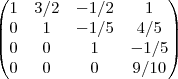
[tex]\begin{pmatrix}
a ultima linha da matriz deveria ser toda nula,pois temos tres incgnitas(a,b,c),sistema e incompativel,nao tem soluçao...e como tem-se 0=9/10,caimos em uma incoerencia,uma contradiçao...logo o vetor v,nao pode ser tomado como uma combinaçao linear dos vetores deW=[....]...logo o vetor v,nao pertence ao subespaço gerado pela base W...
ps-costumo errar em contas,pisso e bom refaze-las...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por Raffz » Seg Nov 24, 2014 14:27
por Raffz » Seg Nov 24, 2014 14:27
Agradeço pela ajuda. Agora compreendi o que aconteceu:
De início, permutei a L2 com a L1, isso é permitido porém é provável que isso tenh atrapalhado meus cálculos e errei em alguma besteira...
Fiz novamente o escalonamento, desta vez sem fazer essa permutação, e realmente, a última linha dá uma incoerência, o que mostra que o vetor não pertence a W.
Vlw!
-
Raffz
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Nov 24, 2014 02:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Determinar um Vetor
por fernandosoares » Ter Abr 14, 2015 10:04
- 1 Respostas
- 2182 Exibições
- Última mensagem por DanielFerreira

Qua Abr 15, 2015 23:58
Geometria Analítica
-
- [Subespaço Vetorial] Subespaço envolvendo matrizes
por hyge » Qua Mai 02, 2018 17:04
- 2 Respostas
- 10991 Exibições
- Última mensagem por adauto martins

Dom Mai 06, 2018 12:28
Álgebra Linear
-
- [Subespaço Vetorial] Verificar que é o conjunto é subespaço
por anderson_wallace » Seg Dez 30, 2013 17:56
- 3 Respostas
- 4687 Exibições
- Última mensagem por Renato_RJ

Ter Dez 31, 2013 14:00
Álgebra Linear
-
- [retas que pertence ao plano]
por lucasdemirand » Dom Set 01, 2013 00:08
- 2 Respostas
- 1528 Exibições
- Última mensagem por lucasdemirand

Dom Set 01, 2013 12:41
Álgebra Linear
-
- [CURVAS] ângulo entre vetor tangente e vetor posição
por inkz » Ter Nov 20, 2012 01:24
- 5 Respostas
- 4902 Exibições
- Última mensagem por LuannLuna

Qui Nov 29, 2012 15:05
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


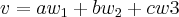 ...
...![(2,3,-7,3)=a(2,1,0,3)+b(3,-1,5,2)+c(-1,0,2,1)...[tex]\Rightarrow 2a+3b-c=2,a-b=3,5b+2c=-7,3a+2b+c=3... (2,3,-7,3)=a(2,1,0,3)+b(3,-1,5,2)+c(-1,0,2,1)...[tex]\Rightarrow 2a+3b-c=2,a-b=3,5b+2c=-7,3a+2b+c=3...](/latexrender/pictures/94a2085d4d392bfa25ac50f419bc620b.png) sao as equaçoes,colocando-as em uma matriz completa ...
sao as equaçoes,colocando-as em uma matriz completa ...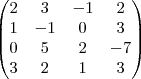 ,escalonandom,teremos
,escalonandom,teremos