 por palliativos » Dom Nov 16, 2014 20:35
por palliativos » Dom Nov 16, 2014 20:35
Olá pessoal, preciso resolver a equação abaixo usando o método de coeficientes indeterminados.
Já começa que não sei se estou usando a equação chute certa. To usando y=(ax+b)e^(-x)
Se está certo até aí, creio que meu erro está na álgebra, porque chega no final fico com e^(-x)(-4a)=-3xe^(-x). Aí eu ficaria com a=3x/4, mas pelo que vi no wolfram já está errado, deveria dar 3x/8.
Eis a equação: y''-2y'-3y=-3xe^(-x)
Desde já fico agradecido.
-
palliativos
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Nov 08, 2014 18:33
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por adauto martins » Qua Nov 19, 2014 12:06
por adauto martins » Qua Nov 19, 2014 12:06
faz-se
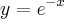
tem-se
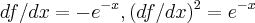
...

x=0...y=1
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equações Diferenciais-Redução de Ordem uma ajudinha=)
por Garota nerd » Dom Nov 25, 2012 23:59
- 2 Respostas
- 1947 Exibições
- Última mensagem por Garota nerd

Seg Nov 26, 2012 23:32
Cálculo: Limites, Derivadas e Integrais
-
- Equações diferenciais: ordem, tipo e grau
 por luanavsr » Qui Set 05, 2013 14:56
por luanavsr » Qui Set 05, 2013 14:56
- 0 Respostas
- 1333 Exibições
- Última mensagem por luanavsr

Qui Set 05, 2013 14:56
Cálculo: Limites, Derivadas e Integrais
-
- EDO de Segunda Ordem
por OtavioBonassi » Ter Nov 15, 2011 11:45
- 0 Respostas
- 1258 Exibições
- Última mensagem por OtavioBonassi

Ter Nov 15, 2011 11:45
Sistemas de Equações
-
- derivada de segunda ordem
por lgbmp » Sex Set 03, 2010 19:25
- 2 Respostas
- 3033 Exibições
- Última mensagem por lgbmp

Seg Set 06, 2010 13:35
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada de segunda ordem]
por spektroos » Sáb Nov 24, 2012 23:43
- 2 Respostas
- 2228 Exibições
- Última mensagem por spektroos

Dom Nov 25, 2012 02:39
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


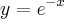 tem-se
tem-se 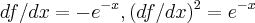 ...
... x=0...y=1
x=0...y=1
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.