 por Fernandobertolaccini » Seg Nov 03, 2014 17:32
por Fernandobertolaccini » Seg Nov 03, 2014 17:32
Mostre que:
![\int_{0}^{b/2}x^2\sqrt[]{b^2-x^2}dx = \frac{b^4}{16}(\frac{\pi}{3}-\frac{\sqrt[]{3}}{4}) \int_{0}^{b/2}x^2\sqrt[]{b^2-x^2}dx = \frac{b^4}{16}(\frac{\pi}{3}-\frac{\sqrt[]{3}}{4})](/latexrender/pictures/cb6496bebfdf2f770b9a36f48460ae22.png)
Muito Obrigado !!
-
Fernandobertolaccini
- Colaborador Voluntário

-
- Mensagens: 100
- Registrado em: Qui Mai 01, 2014 10:27
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Licenciatura em Física
- Andamento: cursando
 por young_jedi » Seg Nov 03, 2014 23:05
por young_jedi » Seg Nov 03, 2014 23:05
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Integral por substituição trigonométrica.
por ClaudioSP » Qui Out 08, 2009 12:25
- 1 Respostas
- 3748 Exibições
- Última mensagem por ClaudioSP

Qui Out 08, 2009 14:25
Cálculo: Limites, Derivadas e Integrais
-
- integral por substituiçao trigonometrica 3
por beel » Dom Nov 27, 2011 18:24
- 3 Respostas
- 2889 Exibições
- Última mensagem por LuizAquino

Seg Nov 28, 2011 16:44
Cálculo: Limites, Derivadas e Integrais
-
- integral- substituiçao trigonometrica 4
por beel » Dom Nov 27, 2011 18:29
- 1 Respostas
- 2057 Exibições
- Última mensagem por LuizAquino

Seg Nov 28, 2011 16:26
Cálculo: Limites, Derivadas e Integrais
-
- Integral por substituição trigonométrica
por Crist » Seg Nov 12, 2012 20:46
- 1 Respostas
- 1481 Exibições
- Última mensagem por e8group

Qui Nov 15, 2012 15:38
Cálculo: Limites, Derivadas e Integrais
-
- [Integral] Substituição Trigonométrica
por klueger » Qua Mar 06, 2013 23:03
- 4 Respostas
- 3652 Exibições
- Última mensagem por Russman

Qui Mar 07, 2013 01:45
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{0}^{b/2}x^2\sqrt[]{b^2-x^2}dx = \frac{b^4}{16}(\frac{\pi}{3}-\frac{\sqrt[]{3}}{4}) \int_{0}^{b/2}x^2\sqrt[]{b^2-x^2}dx = \frac{b^4}{16}(\frac{\pi}{3}-\frac{\sqrt[]{3}}{4})](/latexrender/pictures/cb6496bebfdf2f770b9a36f48460ae22.png)

![\int_{0}^{b/2}x^2\sqrt[]{b^2-x^2}dx = \frac{b^4}{16}(\frac{\pi}{3}-\frac{\sqrt[]{3}}{4}) \int_{0}^{b/2}x^2\sqrt[]{b^2-x^2}dx = \frac{b^4}{16}(\frac{\pi}{3}-\frac{\sqrt[]{3}}{4})](/latexrender/pictures/cb6496bebfdf2f770b9a36f48460ae22.png)

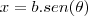








 .
.
 :
: