![\[f(x,y)= e^{-xy}\]](/latexrender/pictures/b6474f528d0622be5ef02fd1e90a0a94.png "\[f(x,y)= e^{-xy}\]")
no ponto (0,2) tem valor 1.Eu tentei resolver para cair num sistema de equações para encontrar as direções a e b, fazendo o produto escalar do vetor gradiente pelo vetor unitário de direções <a,b> e igualando isso a 1:
![\[D_{u}f(x,y)=1 \rightarrow grad f(x,y)\cdot <a,b> = 1\]](/latexrender/pictures/669f91ff8d72082fb1b1f16ae135ffac.png "\[D_{u}f(x,y)=1 \rightarrow grad f(x,y)\cdot <a,b> = 1\]")
![\[grad f(x,y) = \frac{\partial f}{\partial x}i + \frac{\partial f}{\partial x}j\]](/latexrender/pictures/813d192820a088667434ef7fd9b033d7.png "\[grad f(x,y) = \frac{\partial f}{\partial x}i + \frac{\partial f}{\partial x}j\]")
![\[gradf(x,y)=-y^{2}e^{-xy}i+e^{-xy}(1-x)j\]](/latexrender/pictures/35636b21998d27aec70af8c0f7a28600.png "\[gradf(x,y)=-y^{2}e^{-xy}i+e^{-xy}(1-x)j\]")
![\[gradf(0,2)=-2^{2}e^{-0*2}i+e^{-0*2}(1-0)j = -4i+j = <-4,1>\]](/latexrender/pictures/f96b93e0c29fdbf8456ea918e651aaaa.png "\[gradf(0,2)=-2^{2}e^{-0*2}i+e^{-0*2}(1-0)j = -4i+j = <-4,1>\]")
![\[<-4,1>\cdot <a,b>=1\]](/latexrender/pictures/ff51a6d0d5935f4878981bc293538370.png "\[<-4,1>\cdot <a,b>=1\]")
![\[-4a+b=1\]](/latexrender/pictures/f8285dbbcd312c017d34bc2afa47e260.png "\[-4a+b=1\]")
Eu cheguei nessa equação que relaciona as direções do vetor, mas falta alguma outra equação para resolver o sistema e encontrar as direções. Alguém poderia me dar uma ajuda por favor?
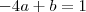
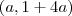
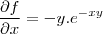
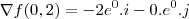
por 
.
: