A soma dos três números que forma uma P.A. crescente é 36. Determine esses números, sabendo que, se somarmos 6 unidades ao último, eles passam a constituir uma P.G..
Estou meio perdido na resolução, mas explicar até onde consegui desenvolver..

Utilizano a Soma da P.A.:

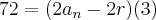
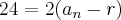
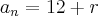
A razão da P.A. não é a mesma da P.G, mas o 1º termo
 é o mesmo.
é o mesmo.Como prosseguir com os cálculos?
Até mais.
Até mais.



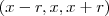


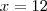
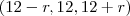


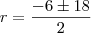
 (Não convém) ou
(Não convém) ou  .
.



 .
.



