usando a formula mmc(a,b)*mdc(a,b)=a*b encontro mmc(a,b)=216, fatorando 216= 2³.
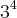 e 12= 2³.3 minha duvida agora é como achar os valores de a e b.
e 12= 2³.3 minha duvida agora é como achar os valores de a e b.
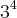 e 12= 2³.3 minha duvida agora é como achar os valores de a e b.
e 12= 2³.3 minha duvida agora é como achar os valores de a e b.

Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes

 .
.
 :
: