 por matmatco » Qua Ago 13, 2014 15:15
por matmatco » Qua Ago 13, 2014 15:15
determine dois numeros inteiros positivos a<= b tais que ab=2592 e mdc(a,b)=12
usando a formula mmc(a,b)*mdc(a,b)=a*b encontro mmc(a,b)=216, fatorando 216= 2³.
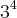
e 12= 2³.3 minha duvida agora é como achar os valores de a e b.
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
 por Russman » Qua Ago 13, 2014 18:34
por Russman » Qua Ago 13, 2014 18:34
Muito bem. Se mdc(a,b)=12 significa que a e b são múltiplos de 12. Assim, escrevemos
a=12n
b=12m
Agora, se ab=2592 então nm=18 = 2.3^2.
Já que n e m devem ser inteiros temos as possibilidades (n,m) = (2,9),(9,2),(6,3),(3,6),(1,18),(18,1).
Escolhendo, por exemplo n=6 e m=3 temos a = 72 e b=36.
Na verdade existem seis valores possíveis para a e b
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por matmatco » Qua Ago 13, 2014 18:40
por matmatco » Qua Ago 13, 2014 18:40
entendi, muito obrigado Russman
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
Voltar para Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
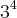 e 12= 2³.3 minha duvida agora é como achar os valores de a e b.
e 12= 2³.3 minha duvida agora é como achar os valores de a e b.
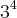 e 12= 2³.3 minha duvida agora é como achar os valores de a e b.
e 12= 2³.3 minha duvida agora é como achar os valores de a e b.
