duvida - derivada de constante

por **hallory03** » Dom Jun 22, 2014 16:42

Porque a derivada de uma constante é 0(zero) e nao 1(um)?

F(x) = ${x}^{1}$ -> F'(x)= 1

o 1 que esta no expoente desce multiplicando o x, e o x fica elevado a zero porque subtrai 1 do expoente e todo numero elevado a zero é igual a 1, logo 1x1 =1

mas quando temos uma constante a regra diz que é zero.
Onde esta o erro do meu modo de pensamento supondo que o x fosse uma constante como por exemplo 3, o resultado seria 0(zero) e nao 1(um)?!

Outra duvida: quando uma constante tem um um expoente maior que 1(um) por exemplo ${\pi}^{3}$ , a derivada é zero ou resolvemos como se fosse uma incógnita?

por **e8group** » Dom Jun 22, 2014 18:03

Antes de tudo f(x) = x^1 = x

; de modo que f(1) = 1^1 = 1

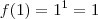e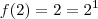

, logo não constante . Prova-se via definição de derivada que 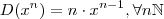$D( x^n) = n \cdot x^{n-1} , \forall n \mathbb{N}$ e também que 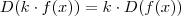$D(k \cdot f(x)) = k \cdot D(f(x))$ (k constante ) . Mas como gosto de contar objetos começando pelo zero , vou incluir o zero aos naturais , o que nos dá 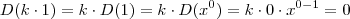$D(k \cdot 1) = k \cdot D(1) = k \cdot D(x^0) = k \cdot 0 \cdot x^{0-1} = 0$ . A derivada de

no ponto

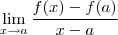é dada pelo limite $\lim_{x \to a } \frac{f(x) - f(a)}{x-a}$ . (Se o limite existir f'(a) existe ; caso contrário não ) . Ora , em particular se

for constante (i.e, f(x) = k

= constante , para todo x ) temos que f(x) = f(a) = k

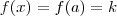; logo

e assim $\lim_{x \to a } \frac{f(x) - f(a)}{x-a} = 0$ .(Note que este limite não é indeterminado , enquanto o x -a

se aproxima de zero ; o numerador já vale zero há mt tempo ) . E outra ...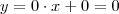

Geometricamente , o gráfico de uma função constante é uma reta paralela à reta $y = 0 \cdot x + 0 = 0$ (eixo x) Como uma reta é tangente a si própria , logo o coeficiente da reta tangente ( derivada de f em algum ponto a ) vale o coeficiente angular desta reta que neste caso

.

por **hallory03** » Qui Jun 26, 2014 17:31

ok, entendi o principio, abriu uma luz.
Obg santhiago!

duvida - derivada de constante

duvida - derivada de constante

duvida - derivada de constante

Re: duvida - derivada de constante

Re: duvida - derivada de constante

Quem está online