 por hallory03 » Dom Jun 22, 2014 16:42
por hallory03 » Dom Jun 22, 2014 16:42
Porque a derivada de uma constante é 0(zero) e nao 1(um)?
F(x) =

-> F'(x)= 1
o 1 que esta no expoente desce multiplicando o x, e o x fica elevado a zero porque subtrai 1 do expoente e todo numero elevado a zero é igual a 1, logo 1x1 =1
mas quando temos uma constante a regra diz que é zero.
Onde esta o erro do meu modo de pensamento supondo que o x fosse uma constante como por exemplo 3, o resultado seria 0(zero) e nao 1(um)?!
Outra duvida: quando uma constante tem um um expoente maior que 1(um) por exemplo

, a derivada é zero ou resolvemos como se fosse uma incógnita?
-
hallory03
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Jun 22, 2014 16:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por e8group » Dom Jun 22, 2014 18:03
por e8group » Dom Jun 22, 2014 18:03
Antes de tudo

; de modo que
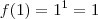
e
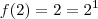
, logo não constante . Prova-se via definição de derivada que
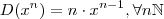
e também que
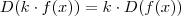
(k constante ) . Mas como gosto de contar objetos começando pelo zero , vou incluir o zero aos naturais , o que nos dá
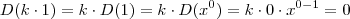
. A derivada de

no ponto

é dada pelo limite
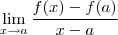
. (Se o limite existir f'(a) existe ; caso contrário não ) . Ora , em particular se

for constante (i.e,

= constante , para todo x ) temos que
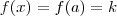
; logo

e assim

.(Note que este limite não é indeterminado , enquanto o

se aproxima de zero ; o numerador já vale zero há mt tempo ) . E outra ...
Geometricamente , o gráfico de uma função constante é uma reta paralela à reta
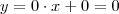
(eixo x) Como uma reta é tangente a si própria , logo o coeficiente da reta tangente ( derivada de f em algum ponto a ) vale o coeficiente angular desta reta que neste caso

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por hallory03 » Qui Jun 26, 2014 17:31
por hallory03 » Qui Jun 26, 2014 17:31
ok, entendi o principio, abriu uma luz.
Obg santhiago!
-
hallory03
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Dom Jun 22, 2014 16:25
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Variação Constante
por Andreza » Ter Fev 28, 2012 19:04
- 2 Respostas
- 2453 Exibições
- Última mensagem por MarceloFantini

Ter Fev 28, 2012 21:53
Funções
-
- calcular constante no limite
por uefs » Qui Abr 17, 2014 00:23
- 8 Respostas
- 4724 Exibições
- Última mensagem por e8group

Sáb Abr 19, 2014 21:24
Cálculo: Limites, Derivadas e Integrais
-
- Triangulo e quadrado, perimetro constante
 por heldersmd » Sáb Set 15, 2012 12:42
por heldersmd » Sáb Set 15, 2012 12:42
- 1 Respostas
- 1500 Exibições
- Última mensagem por young_jedi

Sáb Set 15, 2012 14:54
Geometria Plana
-
- Trabalho realizado por uma força não constante
por Crist » Sex Nov 30, 2012 12:57
- 4 Respostas
- 2231 Exibições
- Última mensagem por Crist

Ter Dez 04, 2012 09:06
Cálculo: Limites, Derivadas e Integrais
-
- [Aplicação constante] Forma genérica da função
por CBRJ » Ter Abr 09, 2013 23:51
- 4 Respostas
- 3401 Exibições
- Última mensagem por CBRJ

Qua Abr 10, 2013 01:36
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 -> F'(x)= 1
-> F'(x)= 1 , a derivada é zero ou resolvemos como se fosse uma incógnita?
, a derivada é zero ou resolvemos como se fosse uma incógnita?

 ; de modo que
; de modo que 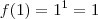 e
e 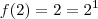 , logo não constante . Prova-se via definição de derivada que
, logo não constante . Prova-se via definição de derivada que 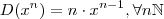 e também que
e também que 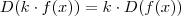 (k constante ) . Mas como gosto de contar objetos começando pelo zero , vou incluir o zero aos naturais , o que nos dá
(k constante ) . Mas como gosto de contar objetos começando pelo zero , vou incluir o zero aos naturais , o que nos dá 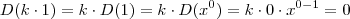 . A derivada de
. A derivada de  no ponto
no ponto  é dada pelo limite
é dada pelo limite 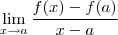 . (Se o limite existir f'(a) existe ; caso contrário não ) . Ora , em particular se
. (Se o limite existir f'(a) existe ; caso contrário não ) . Ora , em particular se  = constante , para todo x ) temos que
= constante , para todo x ) temos que 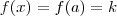 ; logo
; logo  e assim
e assim  .(Note que este limite não é indeterminado , enquanto o
.(Note que este limite não é indeterminado , enquanto o  se aproxima de zero ; o numerador já vale zero há mt tempo ) . E outra ...
se aproxima de zero ; o numerador já vale zero há mt tempo ) . E outra ... 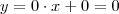 (eixo x) Como uma reta é tangente a si própria , logo o coeficiente da reta tangente ( derivada de f em algum ponto a ) vale o coeficiente angular desta reta que neste caso
(eixo x) Como uma reta é tangente a si própria , logo o coeficiente da reta tangente ( derivada de f em algum ponto a ) vale o coeficiente angular desta reta que neste caso  .
.